OSTrack

简介

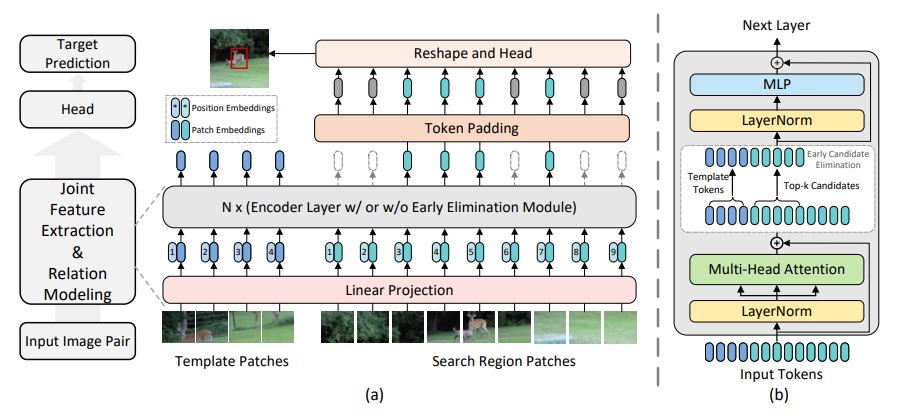
论文来源: Joint Feature Learning and Relation Modeling for Tracking: A One-Stream Framework

当前流行的各种模型都是将模板提取与区域搜索分成两个分支, 再进行关系建模, 因而在提取特征阶段难以感知目标与背景区别. 为了解决该问题, 作者提出了一种单流跟踪框架, 以统一特征学习与关系建模. 由于该框架是高度并行的, 因此计算效率极高.

方法

对于模板 $z \in \mathbb{R}^{3 \times H_z \times W_z}$ , 搜索区域 $x \in \mathbb{R}^{3 \times H_x \times W_x}$ , 它们首先被展平为 patch: $z_p \in \mathbb{R}^{N_z \times (3 \cdot P^2)}, x_p \in \mathbb{R}^{N_x \times (3 \cdot P^2)}$ , 其中 $P \times P$ 是每个 patch 的分辨率, $N_z = H_z W_z / P^2, N_x = H_x W_x / P^2$ 是 patch 数量. 之后, 使用矩阵 $\bm E$ 进行投影, 转化为 $D$ 维特征空间, 得到令牌序列, 如下所示:

\begin{array}{ll} \bm{H}_z^0 = [z_p^1 \bm{E}; z_p^2 \bm{E}; \cdots; z_p^{N_z} \bm{E}] + \bm{P}_z, \bm{E} \in \mathbb{R}^{(3 \cdot P^2) \times D}, \bm{P}_z \in \mathbb{R}^{N_z \times D} \\ \bm{H}_x^0 = [x_p^1 \bm{E}; x_p^2 \bm{E}; \cdots; x_p^{N_x} \bm{E}] + \bm{P}_x, \bm{P}_x \in \mathbb{R}^{N_x \times D} \end{array}

该投影的输出称为 patch 嵌入, $\bm{P}_x, \bm{P}_z$ 是可学习的一维位置嵌入. 作者还尝试向其中加入身份嵌入, 用以区分 patch 是模板还是搜索区域, 但经过消融实验发现没有显著提升, 因而去除了该部分.

将两个令牌序列连接, 得到 $\bm{E}_{zx}^0 = [\bm{E}_z^0; \bm{E}_x^0]$ , 并送入编码器中, 为了使模型高度并行化, 作者使用了自注意力.

A = Softmax(\frac{\bm{Q}\bm{K}^\top}{\sqrt{d_k}}) \cdot \bm{V} = Softmax(\frac{[\bm{Q}_z;\bm{Q}_x] [\bm{K}_z;\bm{K}_x]^\top}{\sqrt{d_k}}) \cdot [\bm{V}_z;\bm{V}_x]

下标 $z, x$ 分别表示模板与搜索区域, 上述公式里的自注意权重计算可以扩展为:

\large \begin{array}{ll} & Softmax(\frac{[\bm{Q}_z;\bm{Q}_x] [\bm{K}_z;\bm{K}_x]^\top}{\sqrt{d_k}}) \\ =& Softmax(\frac{[\bm{Q}_z\bm{K}_z^\top, \bm{Q}_z\bm{K}_x^\top; \bm{Q}_x\bm{K}_z^\top, \bm{Q}_x\bm{K}_x^\top]}{\sqrt{d_k}}) \\ \triangleq & [\bm{W}_{zz}, \bm{W}_{zx}; \bm{W}_{xz}, \bm{W}_{xx}] \end{array}

乘上 $V$ 后, 得到令牌序列

A = [\bm{W}_{zz} \bm{V}_z + \bm{W}_{zx} \bm{V}_x; \bm{W}_{xz} \bm{V}_z + \bm{W}_{xx} \bm{V}_x]

$\bm{W}_{xz} \bm{V}_z$ 负责关系建模, $\bm{W}_{xx} \bm{V}_x$ 负责特征提取, 即仅需使用自注意力就可以同时获取模板与图像的关系和图像内部联系.

为了降低运算量, 作者设计了候选淘汰机制, 它被集成在编码器中. 我们给每个模板 patch 设置一个标记 $\bm{h}_z^i, 1 \leq i \leq N_z$ :

\bm{h}_z^i = Softmax(\frac{\bm{q}_i \cdot [\bm{K}_z; \bm{K}_x]^\top}{\sqrt{d}}) \cdot \bm{V} = [\bm{w}_z^i; \bm{w}_x^i] \cdot \bm{V}

其中 $\bm{q}_i$ 是 $\bm{h}_z^i$ 的查询向量, 注意力权重 $\bm{w}_x^i$ 表示模板区域 $\bm{h}_z^i$ 与搜索区域的相似度. 然而, 模板通常会包括背景区域, 这会在计算中引入噪声, 因此不应简单地将候选区域与各个模板部分的相似度相加, 作者使用了中心区域的相似度来代表整体相似度:

\bm{w}_x^{\phi}, \phi = \left\lfloor \frac{W_z}{2} \right\rfloor + W_z \cdot \left\lfloor \frac{H_z}{2} \right\rfloor

考虑到 ViT 中使用了多头自注意力, 因而我们将得到多个相似度分数, 使用平均数来表示最终相似度:

\bar{w}_x^\phi = \frac1M \sum\limits_{m=1}^{M} w_x^\phi(m)

我们一般认为模板与候选区域相似度越大, 该候选区域就是待追踪目标的可能性越大, 因而我们只需要保留前 $k$ 个相似度最大的区域, 淘汰其他区域. 淘汰操作在多头注意力之后, 如上图右侧所示. 然而我们不应当直接删除这些区域, 因为这会打乱 patch 顺序, 正确的做法应当是填充零.

最后, 将搜索区域序列转换为二维特征图, 使用全卷积网络 $(L$ 个 $Conv-BN-ReLU$ 层 $)$ , 得到分类得分 $\bm{P} \in [0, 1]^{\frac{H_x}P \times \frac{W_x}P}$ , 局部偏移 $\bm{O} \in [0, 1)^{2 \times \frac{H_x}P \times \frac{W_x}P}$ 用于补偿分辨率降低和归一化边界框 $\bm{S} \in [0, 1]^{2 \times \frac{H_x}P \times \frac{W_x}P}$ 造成的误差, 分类得分最高的位置被认定为目标位置, 即 $(x_d, y_d) = \argmax _{(x, y)}\bm{P}_{xy}$ , 最终目标框为:

\left \{ \begin{array}{ll} x = x_d + \bm{O}(0, x_d, y_d) \\ y = y_d + \bm{O}(1, x_d, y_d) \\ w = \bm{S}(0, x_d, y_d) \\ h = \bm{S}(1, x_d, y_d) \end{array} \right.

对于损失函数, 同时使用分类损失与回归损失, 使用加权焦点损失进行分类, 通过预测边界框, 使用 $l1$ 损失与 $IoU$ 损失:

L_{track} = L_{cls} + \lambda_{iou} L_{iou} + \lambda_{L_1}L_1

代码解析

源码地址: https://github.com/botaoye/OSTrack, 模型代码在 ./lib/models 文件夹中.

按照正常人的思路, ostrack.py 就是模型文件, 现在我们查看该文件, 不难发现, 其中最重要的就是 self.backbone 和 self.forward_head.

先看 backbone, 通过检查调用可以发现其实际上是 VisionTransformerCE, 集成关系为: VisionTransformerCE-VisionTransformer-BaseBackbone.

首先查看 base_backbone.py 文件, 里面定义了基础骨干网络, 在构造函数中定义了图像尺寸, 嵌入层等

def __init__(self):
    super().__init__()

    # for original ViT
    # 位置嵌入, 初始为空
    self.pos_embed = None
    # 图片尺寸
    self.img_size = [224, 224]
    # patch 大小
    self.patch_size = 16
    # 嵌入层维数
    self.embed_dim = 384

    # 拼接模式为直接拼接
    self.cat_mode = 'direct'

    # 模板位置嵌入
    self.pos_embed_z = None
    self.pos_embed_x = None

    # 模板与搜索区域的位置嵌入
    self.template_segment_pos_embed = None
    self.search_segment_pos_embed = None

    self.return_inter = False
    self.return_stage = [2, 5, 8, 11]

    self.add_cls_token = False
    self.add_sep_seg = False

前向过程中调用了 forward_features() 函数, 其输入是模板与搜索区域, 查看该函数源码

def forward_features(self, z, x):
    B, H, W = x.shape[0], x.shape[2], x.shape[3]

    # 切割为 patch
    x = self.patch_embed(x)
    z = self.patch_embed(z)

    # 添加分类令牌
    if self.add_cls_token:
        cls_tokens = self.cls_token.expand(B, -1, -1)
        cls_tokens = cls_tokens + self.cls_pos_embed

    # 添加位置编码
    z += self.pos_embed_z
    x += self.pos_embed_x

    # 添加分段标记
    if self.add_sep_seg:
        x += self.search_segment_pos_embed
        z += self.template_segment_pos_embed

    # 将模板与搜索区域相连接, 此处 x 包括模板与搜索区域, 之后会分开
    x = combine_tokens(z, x, mode=self.cat_mode)
    if self.add_cls_token:
        x = torch.cat([cls_tokens, x], dim=1)

    # 随机丢弃, 该部分在 vit.py 中定义
    x = self.pos_drop(x)

    # 遍历 transformer 编码器 block
    for i, blk in enumerate(self.blocks):
        x = blk(x)

    # 获取区域编码长度
    lens_z = self.pos_embed_z.shape[1]
    lens_x = self.pos_embed_x.shape[1]
    # 先前模板与搜索区域被连接到一起, 此处分开
    x = recover_tokens(x, lens_z, lens_x, mode=self.cat_mode)

    aux_dict = {"attn": None}
    return self.norm(x), aux_dict

注意到里面将 $x, z$ 转为 patch, 因此查看 patch 代码, 在 patch_embed.py 中.

def forward(self, x):
    # allow different input size
    # B, C, H, W = x.shape
    # _assert(H == self.img_size[0], f"Input image height ({H}) doesn't match model ({self.img_size[0]}).")
    # _assert(W == self.img_size[1], f"Input image width ({W}) doesn't match model ({self.img_size[1]}).")
    # 将原始图片转化为特征图, 如果按照默认尺寸输入, 则最终维数为: [batch_size, 768, 14, 14]
    x = self.proj(x)
    # 将特征图展平
    if self.flatten:
        x = x.flatten(2).transpose(1, 2)  # BCHW -> BNC, N 为 patch 数量
    x = self.norm(x)
    return x

可以看出最终输出的维数是 $x \in \mathbb{R}^{B \times N_x \times D}$ .

此时还剩下 finetune_track() 这个函数没用到, 实际上该函数是在 ostrack.py 的 build_ostrack() 函数中调用的, 用于对模型进行微调.

在这之前需要先查看 vit_ce.py 的部分代码, 这是 ViT 的实现代码, 后面的 ce 表示候选消除. 其中的 VisionTransformer 类继承了上面的主干网络, 其构造函数中定义的一些参数将会在之后用到. 我们只需要关注以下几个参数.

# 分类器标记
self.cls_token = nn.Parameter(torch.zeros(1, 1, embed_dim))
# 蒸馏模型的蒸馏标记
self.dist_token = nn.Parameter(torch.zeros(1, 1, embed_dim)) if distilled else None
# 位置编码
self.pos_embed = nn.Parameter(torch.zeros(1, num_patches + self.num_tokens, embed_dim))
self.pos_drop = nn.Dropout(p=drop_rate)

位置编码的维数是 num_patches + self.num_tokens, 其中 self.num_tokens = 2 if distilled else 1 用于留出位置给分类器. 而 self.pos_embed 则可以猜测出其维数含义是: 批大小(使用广播机制自动扩展)-patch数量-特征维数.

再回到 finetune_track() 函数, 现在我们就能更方便的理解各行代码含义. 其中有一行代码是 patch_pos_embed = self.pos_embed[:, patch_start_index:, :], 其中 patch 起始位置一般为 1, 这是因为 self.pos_embed 的第一个是分类器标记, 需要排除.

该函数后半部分的代码用于向 patch 中添加位置编码, 它将原位置编码插值为新的维数, 以应用到模板与搜索区域上来.

def finetune_track(self, cfg, patch_start_index=1):

    search_size = to_2tuple(cfg.DATA.SEARCH.SIZE)
    template_size = to_2tuple(cfg.DATA.TEMPLATE.SIZE)
    new_patch_size = cfg.MODEL.BACKBONE.STRIDE

    self.cat_mode = cfg.MODEL.BACKBONE.CAT_MODE
    self.return_inter = cfg.MODEL.RETURN_INTER
    self.return_stage = cfg.MODEL.RETURN_STAGES
    self.add_sep_seg = cfg.MODEL.BACKBONE.SEP_SEG

    # resize patch embedding
    # 预训练模型的 patch 与现模型不同, 需要使用插值对权重进行处理
    if new_patch_size != self.patch_size:
        print('Inconsistent Patch Size With The Pretrained Weights, Interpolate The Weight!')
        old_patch_embed = {}
        for name, param in self.patch_embed.named_parameters():
            if 'weight' in name:
                param = nn.functional.interpolate(param, size=(new_patch_size, new_patch_size),
                                                    mode='bicubic', align_corners=False)
                param = nn.Parameter(param)
            old_patch_embed[name] = param
        self.patch_embed = PatchEmbed(img_size=self.img_size, patch_size=new_patch_size, in_chans=3,
                                        embed_dim=self.embed_dim)
        self.patch_embed.proj.bias = old_patch_embed['proj.bias']
        self.patch_embed.proj.weight = old_patch_embed['proj.weight']

    # for patch embedding
    # 排除掉分类标签, 此时的维数是: 批大小, patch 数量, 特征维数
    patch_pos_embed = self.pos_embed[:, patch_start_index:, :]
    # 现在的维数是: 批大小, 特征维数, patch 数量
    patch_pos_embed = patch_pos_embed.transpose(1, 2)
    # 三个维数分别是: B-批大小, E-特征数量, Q-patch数量
    B, E, Q = patch_pos_embed.shape
    P_H, P_W = self.img_size[0] // self.patch_size, self.img_size[1] // self.patch_size
    # 将展平的 patch 重新改回二维
    patch_pos_embed = patch_pos_embed.view(B, E, P_H, P_W)

    # for search region
    # 将位置编码改为新的维数
    H, W = search_size
    new_P_H, new_P_W = H // new_patch_size, W // new_patch_size
    search_patch_pos_embed = nn.functional.interpolate(patch_pos_embed, size=(new_P_H, new_P_W), mode='bicubic',
                                                        align_corners=False)
    # 现在的三个维数分别是: B-批大小, Q-patch数量, E-特征数量
    search_patch_pos_embed = search_patch_pos_embed.flatten(2).transpose(1, 2)

    # for template region
    # 此处同理
    H, W = template_size
    new_P_H, new_P_W = H // new_patch_size, W // new_patch_size
    template_patch_pos_embed = nn.functional.interpolate(patch_pos_embed, size=(new_P_H, new_P_W), mode='bicubic',
                                                            align_corners=False)
    template_patch_pos_embed = template_patch_pos_embed.flatten(2).transpose(1, 2)

    # 储存为位置编码, 将被加入到模板与搜索区域中
    self.pos_embed_z = nn.Parameter(template_patch_pos_embed)
    self.pos_embed_x = nn.Parameter(search_patch_pos_embed)

    # for cls token (keep it but not used)
    # 保留分类标签
    if self.add_cls_token and patch_start_index > 0:
        cls_pos_embed = self.pos_embed[:, 0:1, :]
        self.cls_pos_embed = nn.Parameter(cls_pos_embed)

    # separate token and segment token
    # 分段标记, 默认不添加
    if self.add_sep_seg:
        self.template_segment_pos_embed = nn.Parameter(torch.zeros(1, 1, self.embed_dim))
        self.template_segment_pos_embed = trunc_normal_(self.template_segment_pos_embed, std=.02)
        self.search_segment_pos_embed = nn.Parameter(torch.zeros(1, 1, self.embed_dim))
        self.search_segment_pos_embed = trunc_normal_(self.search_segment_pos_embed, std=.02)

    # self.cls_token = None
    # self.pos_embed = None

    if self.return_inter:
        for i_layer in self.return_stage:
            if i_layer != 11:
                norm_layer = partial(nn.LayerNorm, eps=1e-6)
                layer = norm_layer(self.embed_dim)
                layer_name = f'norm{i_layer}'
                self.add_module(layer_name, layer)

了解完基础骨干, 就可以开始看 VisionTransformerCE, 在构造函数中有一个循环, 它首先判断第 $i$ 层是否需要候选消除, 即是否 $i \in ce\_loc$ , ce_loc 是一个数组, 用于判断哪基层需要消除, 一般为 [3, 6, 9], 在各个模型的 YAML 配置文件中可以修改, ce_keep_ratio_i 默认为 1.0, 它表示持有比, 也就是最终保留多少 patch, 默认配置为 0.7, 即移除 $30\%$ 的 patch, 不需要候选消除的层全部为 1.0. 最后, 向 blocks 中添加 CEBlock.

CEBlock 包含了候选消除的功能, 我们先暂时跳过该部分, 阅读 VisionTransformerCE 的 forward_features() 函数, 此部分的重点是对消除后的 tokens 序列进行处理, 让被移除的区域填充零, 并保持原始顺序不变.

def forward_features(self, z, x, mask_z=None, mask_x=None,
                        ce_template_mask=None, ce_keep_rate=None,
                        return_last_attn=False
                        ):
    B, H, W = x.shape[0], x.shape[2], x.shape[3]

    # 将模板与搜索区域转为 patch
    x = self.patch_embed(x)
    z = self.patch_embed(z)

    # attention mask handling
    # B, H, W
    # 注意力掩码处理
    if mask_z is not None and mask_x is not None:
        mask_z = F.interpolate(mask_z[None].float(), scale_factor=1. / self.patch_size).to(torch.bool)[0]
        mask_z = mask_z.flatten(1).unsqueeze(-1)

        mask_x = F.interpolate(mask_x[None].float(), scale_factor=1. / self.patch_size).to(torch.bool)[0]
        mask_x = mask_x.flatten(1).unsqueeze(-1)

        mask_x = combine_tokens(mask_z, mask_x, mode=self.cat_mode)
        mask_x = mask_x.squeeze(-1)

    # 添加分类标签
    if self.add_cls_token:
        cls_tokens = self.cls_token.expand(B, -1, -1)
        cls_tokens = cls_tokens + self.cls_pos_embed

    # 添加位置嵌入
    z += self.pos_embed_z
    x += self.pos_embed_x

    # 添加分段标记
    if self.add_sep_seg:
        x += self.search_segment_pos_embed
        z += self.template_segment_pos_embed

    # 将模板与搜索区域连接
    x = combine_tokens(z, x, mode=self.cat_mode)
    # 分类标签在最前面
    if self.add_cls_token:
        x = torch.cat([cls_tokens, x], dim=1)

    x = self.pos_drop(x)

    lens_z = self.pos_embed_z.shape[1]
    lens_x = self.pos_embed_x.shape[1]

    # 创建全局索引并重复 batch 次
    global_index_t = torch.linspace(0, lens_z - 1, lens_z).to(x.device)
    global_index_t = global_index_t.repeat(B, 1)

    global_index_s = torch.linspace(0, lens_x - 1, lens_x).to(x.device)
    global_index_s = global_index_s.repeat(B, 1)
    removed_indexes_s = []
    for i, blk in enumerate(self.blocks):
        x, global_index_t, global_index_s, removed_index_s, attn = \
            blk(x, global_index_t, global_index_s, mask_x, ce_template_mask, ce_keep_rate)

        if self.ce_loc is not None and i in self.ce_loc:
            removed_indexes_s.append(removed_index_s)

    x = self.norm(x)
    lens_x_new = global_index_s.shape[1]
    lens_z_new = global_index_t.shape[1]

    # 移除部分 tokens 之后的新的模板与搜索区域
    z = x[:, :lens_z_new]
    x = x[:, lens_z_new:]

    if removed_indexes_s and removed_indexes_s[0] is not None:
        removed_indexes_cat = torch.cat(removed_indexes_s, dim=1)

        # 被移除的搜索区域 tokens 数量
        pruned_lens_x = lens_x - lens_x_new
        # 生成全 0 张量, 用以填补移除之后造成的空缺
        pad_x = torch.zeros([B, pruned_lens_x, x.shape[2]], device=x.device)
        x = torch.cat([x, pad_x], dim=1)
        index_all = torch.cat([global_index_s, removed_indexes_cat], dim=1)
        # recover original token order
        C = x.shape[-1]
        # x = x.gather(1, index_all.unsqueeze(-1).expand(B, -1, C).argsort(1))
        # 将 x 按照原本的索引填充到新张量中, 使得新的 tokens 序列仍然有序, 而被移除的区域全 0
        x = torch.zeros_like(x).scatter_(dim=1, index=index_all.unsqueeze(-1).expand(B, -1, C).to(torch.int64), src=x)

    # 此处在实际运行时会直接返回 x
    x = recover_tokens(x, lens_z_new, lens_x, mode=self.cat_mode)

    # re-concatenate with the template, which may be further used by other modules
    # 恢复原本的模板+搜索区域的结构
    x = torch.cat([z, x], dim=1)

    aux_dict = {
        "attn": attn,
        "removed_indexes_s": removed_indexes_s,  # used for visualization
    }

    return x, aux_dict

最后来看实现候选消除的 CEBlock, 我们直接看 forward() 函数. 除了注意力以外, 后面使用了 candidate_elimination() 函数进行消除操作. 其中 attn 来自 attn.py 中的 attn = (q @ k.transpose(-2, -1)) * self.scale 一行, 其中 $\bm{q}, \bm{k} \in \mathbb{R}^{N \times C}$ , 因此 $attn \in \mathbb{R}^{N \times N}$ , 如果用 $t$ 表示模板, $s$ 表示搜索区域, 则 $attn$ 矩阵的具体内容可以表示为:

attn = \begin{pmatrix} t_1 t_1 & \cdots & t_1 t_{lens\_t} & \color{red}t_1 s_1 & \color{red} \cdots & \color{red} t_1 s_{lens\_s} \\ \vdots & \ddots & \vdots & \color{red} \vdots & \color{red} \ddots & \color{red} \vdots \\ t_{lens\_t} t_{lens\_t} & \cdots & t_{lens\_t} t_{lens\_t} & \color{red} t_{lens\_t} s_1 & \color{red} \cdots & \color{red} t_{lens\_t} s_{lens\_s} \\ s_1 t_1 & \cdots & s_1 t_{lens\_t} & s_1 s_1 & \cdots & s_1 s_{lens\_s} \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ s_{lens\_s} t_1 & \cdots & s_{lens\_s} t_{lens\_t} & s_{lens\_s} s_1 & \cdots & s_{lens\_s} s_{lens\_s} \end{pmatrix}

我们只需要右上角 $lens\_ t \times lens\_ s$ 的矩阵, 也就是公式中的红色区域, 于是在 candidate_elimination() 中, 作者使用了 attn_t = attn[:, :, :lens_t, lens_t:], 该代码的含义是取出前 $lens\_t$ 行与第 $lens\_t$ 开始直到末尾的列(起始下标为 $0$ ), 恰好对应右上角区域.

接下来就是 box_mask_z, 它来自 ./lib/utils/ce_utils.py 中的 generate_mask_cond() 函数, 观察代码可以看出它实际上是一个仅中间值取 True, 其他全为 False 的数组, 其作用是取出中间位置的值, 再求多头注意力平均数, 随后使用 sort 降序排列, 取出前 $lens\_keep$ 个 patch, 与模板拼接后返回.

def candidate_elimination(attn: torch.Tensor, tokens: torch.Tensor, lens_t: int, keep_ratio: float, global_index: torch.Tensor, box_mask_z: torch.Tensor):
    """
    Eliminate potential background candidates for computation reduction and noise cancellation.
    Args:
        attn (torch.Tensor): [B, num_heads, L_t + L_s, L_t + L_s], attention weights
        tokens (torch.Tensor):  [B, L_t + L_s, C], template and search region tokens
        lens_t (int): length of template
        keep_ratio (float): keep ratio of search region tokens (candidates)
        global_index (torch.Tensor): global index of search region tokens
        box_mask_z (torch.Tensor): template mask used to accumulate attention weights

    Returns:
        tokens_new (torch.Tensor): tokens after candidate elimination
        keep_index (torch.Tensor): indices of kept search region tokens
        removed_index (torch.Tensor): indices of removed search region tokens
    """
    # 只有搜索区域需要消除
    lens_s = attn.shape[-1] - lens_t
    bs, hn, _, _ = attn.shape

    # 计算出需要保留的 patch 数量
    lens_keep = math.ceil(keep_ratio * lens_s)
    if lens_keep == lens_s:
        return tokens, global_index, None

    # 仅选取模板与搜索区域的相似度
    attn_t = attn[:, :, :lens_t, lens_t:]

    # 使用蒙版选取中心区域
    if box_mask_z is not None:
        box_mask_z = box_mask_z.unsqueeze(1).unsqueeze(-1).expand(-1, attn_t.shape[1], -1, attn_t.shape[-1])
        # attn_t = attn_t[:, :, box_mask_z, :]
        attn_t = attn_t[box_mask_z]
        attn_t = attn_t.view(bs, hn, -1, lens_s)
        attn_t = attn_t.mean(dim=2).mean(dim=1)  # B, H, L-T, L_s --> B, L_s

        # attn_t = [attn_t[i, :, box_mask_z[i, :], :] for i in range(attn_t.size(0))]
        # attn_t = [attn_t[i].mean(dim=1).mean(dim=0) for i in range(len(attn_t))]
        # attn_t = torch.stack(attn_t, dim=0)
    else:
        attn_t = attn_t.mean(dim=2).mean(dim=1)  # B, H, L-T, L_s --> B, L_s

    # use sort instead of topk, due to the speed issue
    # https://github.com/pytorch/pytorch/issues/22812
    # 降序排列
    sorted_attn, indices = torch.sort(attn_t, dim=1, descending=True)

    # 取出前 lens_keep 个候选区域, 其余的为排除区域
    topk_attn, topk_idx = sorted_attn[:, :lens_keep], indices[:, :lens_keep]
    non_topk_attn, non_topk_idx = sorted_attn[:, lens_keep:], indices[:, lens_keep:]

    # 保留的索引和删除的索引
    keep_index = global_index.gather(dim=1, index=topk_idx)
    removed_index = global_index.gather(dim=1, index=non_topk_idx)

    # separate template and search tokens
    # 分离出模板 tokens 与 搜索区域 tokens
    tokens_t = tokens[:, :lens_t]
    tokens_s = tokens[:, lens_t:]

    # obtain the attentive and inattentive tokens
    B, L, C = tokens_s.shape
    # topk_idx_ = topk_idx.unsqueeze(-1).expand(B, lens_keep, C)
    # 只取出保留的区域
    attentive_tokens = tokens_s.gather(dim=1, index=topk_idx.unsqueeze(-1).expand(B, -1, C))
    # inattentive_tokens = tokens_s.gather(dim=1, index=non_topk_idx.unsqueeze(-1).expand(B, -1, C))

    # compute the weighted combination of inattentive tokens
    # fused_token = non_topk_attn @ inattentive_tokens

    # concatenate these tokens
    # tokens_new = torch.cat([tokens_t, attentive_tokens, fused_token], dim=0)
    # 重新拼接到一起
    tokens_new = torch.cat([tokens_t, attentive_tokens], dim=1)

    # 返回值分别是
    # 移除低分区域后的新 tokens
    # 新 tokens 对应的全局索引, 该索引始终不变
    # 被移除的 tokens 对应的全局索引
    return tokens_new, keep_index, removed_index