中间融合及多阶段多提示的鲁棒RGBT追踪

简介

论文: Middle Fusion and Multi-Stage, Multi-Form Prompts for Robust RGB-T Tracking

RGBT 追踪主要受到以下两个阻碍: 1) 性能和效率之间的权衡; 2) 训练数据的稀缺. 为了解决后一个挑战, 一些方法采用提示来微调. 然而这些方法只考虑到模态相关的模式, 而忽略了模态无关的模式, 同时也忽略了开放场景中不同模态的动态可靠性. 本文将提出 M3PT, 一种 RGB-T 提示跟踪方法, 利用中间融合和多模式、多阶段视觉提升来克服上面的挑战, 并平衡性能与效率.

方法

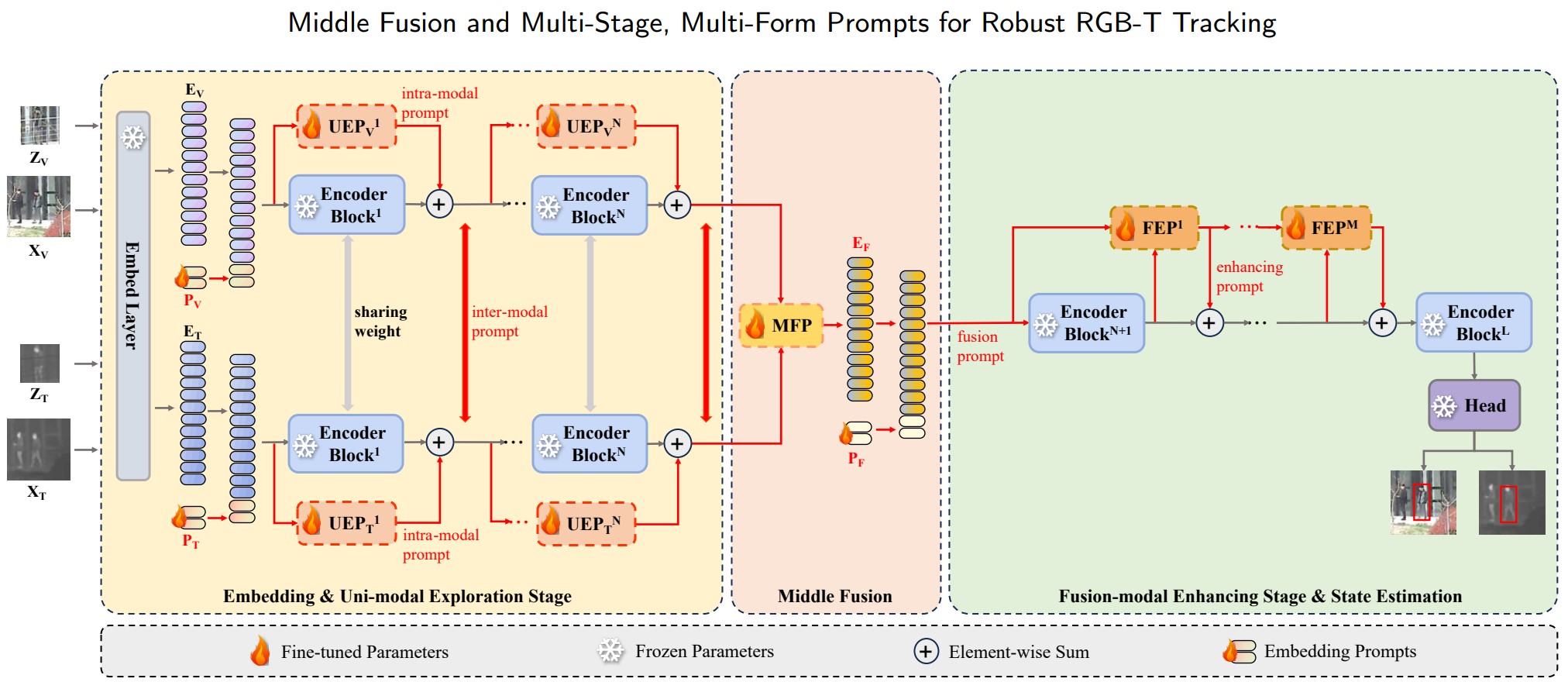
在第一阶段, 使用双流网络分别提取两个单模态特征. 第二阶段主干是增强融合模式特征的单流网络. 中间融合模块位于两者之间, 作者使用了 4 种提示策略将预训练基础模型嵌入到本框架中, 以实现知识迁移. 这些策略分别是:

1. 将来自基础模型主干的 $L$ 个 Transformer Encoder 被分为两组, 分别是 $N$ 个和 $M$ 个 Encoder, 以用于两个阶段的特征提取.

2. 单模态探索提示(UEP)策略将第一组 Encoder 扩展为参数共享的双分支结构, 并逐层并行配置 UEP, 以探索模态无关信息并生成模态内和模态间提示, 使得 Encoder 更好地适应单模态特征建模.

3. 中间融合提示(MFP)策略用以聚合第一个主干输出的结果, 而自己的输出作为第二阶段主干的视觉提示.

4. 融合模态增强提示(FEP)策略逐层配置轻量级提示, 以获得更丰富的融合模态特征表示, 增强在主干网络中前向传播的融合模态特征.

5. 模态感知和阶段感知提示策略分两个阶段将 3 个可学习提示添加到主干输入中, 以指导它们更快地识别当前模态的分布特征.

6. 直接使用基础模型的预测头进行搜索.

单模态探索提示策略(UEP)

UEP 的具体结构如下所示:

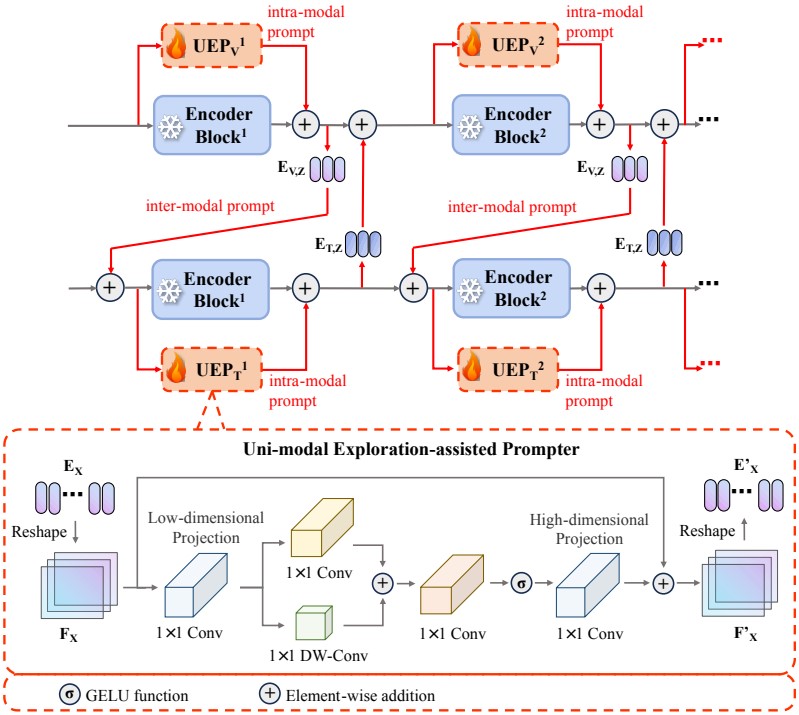
输入的 Token 被记为 $E_X$, 它被 Reshape 为二维并映射到低维特征空间, 并用并行的 $1 \times 1$ 卷积和 DW 卷积(深度可分离卷积)组合成, 随后使用具有 $GELU$ 激活函数的 $1 \times 1$ 卷积层实现局部特征提取, 最后重新映射到高维空间, 并与输入值进行残差连接. 由于特征提取过程在低维进行, 因此 UEP 仅需要少量参数, 作者将热红外和可见光的低维特征空间维数分别设置为 $8, 16$. 除此之外, 还可根据 UEP 的输出生成两种视觉提示: 模态内提示和模态间提示. 以可见光分支为例, 首先提取模态无关特征:

$$P_{V, intra}^n = UEP_V^n(H_V^n) \\ E_V^n = Encoder^n(H_V^n) + P_{V, intra}^n$$

其中下标 $V$ 表示可见光模态, 上标 $n$ 表示层数, $H$ 表示输入的 Token. 此时的 $E_V^n$ 维数是: $E_V^n \in \R^{(N_Z + N_X) \times D} $, 然后将模板 Token 拆出, 最为模板间提示逐元素加到另一模态模板. 下面是论文给出的公式.

$$[E_{V, Z}^n, E_{V, X}^n] = unconcaten(E_V^n) \\ P_{V, inter}^n = E_{V, Z}^n \\ H_{T, Z}^{n+1} = E_{T, Z}^n + P_{V, inter}^n \\$$

上述公式与结构图存在冲突, 若按照结构图, 则第三条公式应改为:

$$H_{T, Z}^n = E_{T, Z}^{n-1} + P_{V, inter}^n$$

中间融合提示策略(MFP)

MFP 的具体结构如下所示:

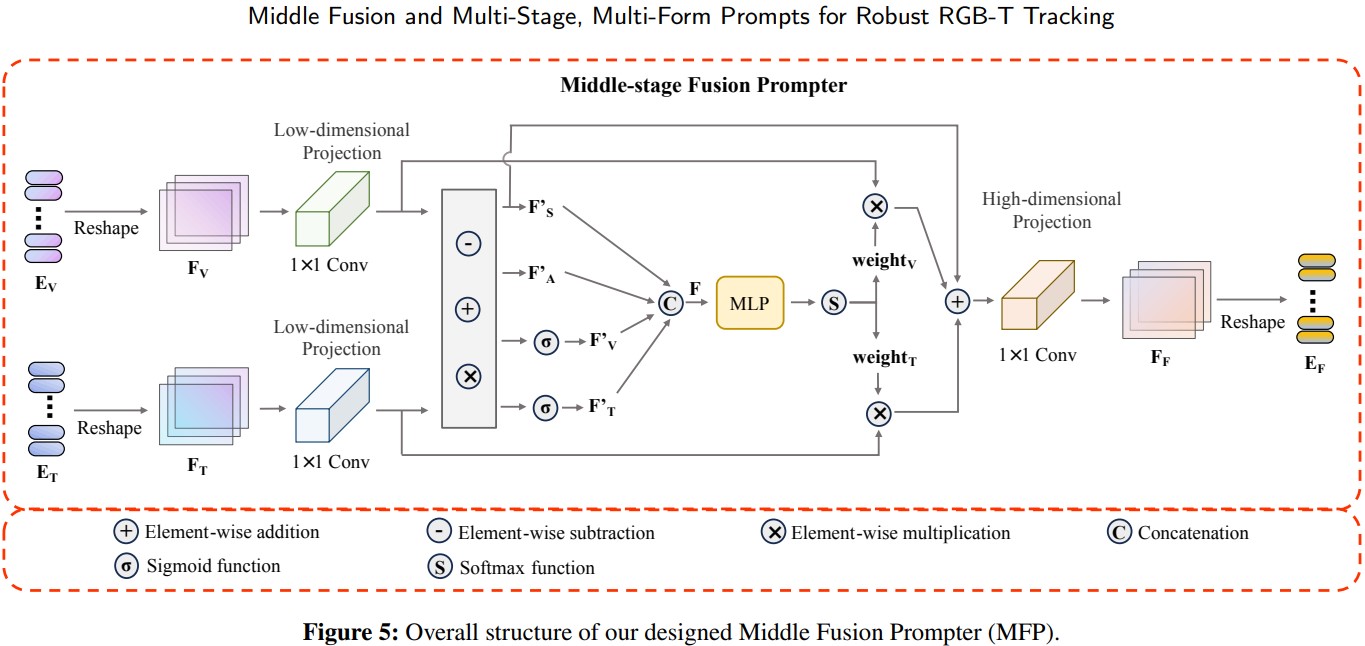
输入 $E_V, E_T$ 被 Reshape 为 $F_V, F_T$, 然后映射到维数为 $16$ 的低维特征空间. 注意这里的两个 $1 \times 1$ 卷积权值不共享, 随后将模态共享与模态无关信息分开:

$$F_S' = (F_{V, L} \times F_{T, L}) \\ F_A' = (F_{V, L} + F_{T, L}) \\ F_V' = Sigmoid(F_{V, L} - F_{T, L}) \\ F_T' = Sigmoid(F_{T, L} - F_{V, L}) \\$$

其中 $F_{V, L}, F_{T, L}$ 分别表示被映射到低维空间的可见光和热红外特征, $F_S'$ 表示模态共享特征, $F_A'$ 表示整体特征. 上面的运算符号均表示逐元素运算. 随后连接以上元素.

$$F = concaten(F_V', F_S', F_A', F_S', F_T') \\ [weight_V, weight_T] = Softmax(fc(F))$$

其中 $fc$ 表示全连接层, 最终融合过程如下:

$$F_{F, L} = F_S' + F_{V, L} \times weight_V + F_{T, L} \times weight_T$$

与一般的权重融合不同, 作者额外加上了 $F_S'$, 主要是为了防止低权重位置有用信息被抑制, 而这种低权重信息大都属于模态共享信息. 最后, 融合信息被重新映射回原始维数并整合成 Token.

融合模态增强提示策略(FEP)

FEP 模块的输入包括 Token 和编码器输出:

$$P^m = FEP^{m-N}(H^m, Encoder^m(H^m)), m=N+1 \\ P^m = FEP^{m-N}(P^{m-1}, Encoder^m(H^m)), m>N+1 \\ H^{m+1} = Encoder^m(H^m) + P^m, m>N+1$$

从上面的公式可以看出, 对于第一个 FEP 模块, 其输入是 Token 和第 $(N+1)$ 层 Encoder 输出(前 $N$ 个 Encoder 位于第一阶段主干中). 对于之后的 FEP 模块, 其输入是上一层 FEP 模块的输出和当前 Encoder 输出.

此处序号存在疑问, 按照论文所讲, Transformer 的 $L$ 个 Encoder 被分为 $N+M$ 个, 归为第一阶段和第二阶段主干使用. 而第二阶段 FEP 模块与 Encoder 是一一对应的, FEP 模块下标范围是 $1 \sim M$, 则 Encoder 的下标应对应 $(N+1) \sim (N+M)$, 即至少有 $M$ 个 Encoder 与 FEP 模块一一对应, 此时 $L$ 个 Encoder 已被全部分配完毕, 则最后一个 Encoder 是凭空多出来的.

模态感知和阶段感知提示策略

模型中一共出现 $3$ 次该类型提示, 分别是 $P_V, P_T, P_F$, 前两个在第一阶段特征提取, 后者在第二阶段特征提取. 三个提示均为可学习的, 并且不参与其他提示策略. 以可见光分支的 UEP 为例, 输入 Encoder 的参数为 $[E_V, P_V]$, 而进入 UEP 模块的则为 $P_V$, 若 UEP 模块输出为 $E_V'$, 则最终输出会被再次加上提示: $[E_V', P_V]$. 也就是说, 每当经过其他提示模块, $P$ 就会被分离出来, 最后添加到模块输出中.

损失函数

损失函数较为传统, 即 IoU 损失与 L1 损失.

$$L = L_{cls} + \lambda_{iou} L_{giou} + \lambda_{L1} L_{L1}$$