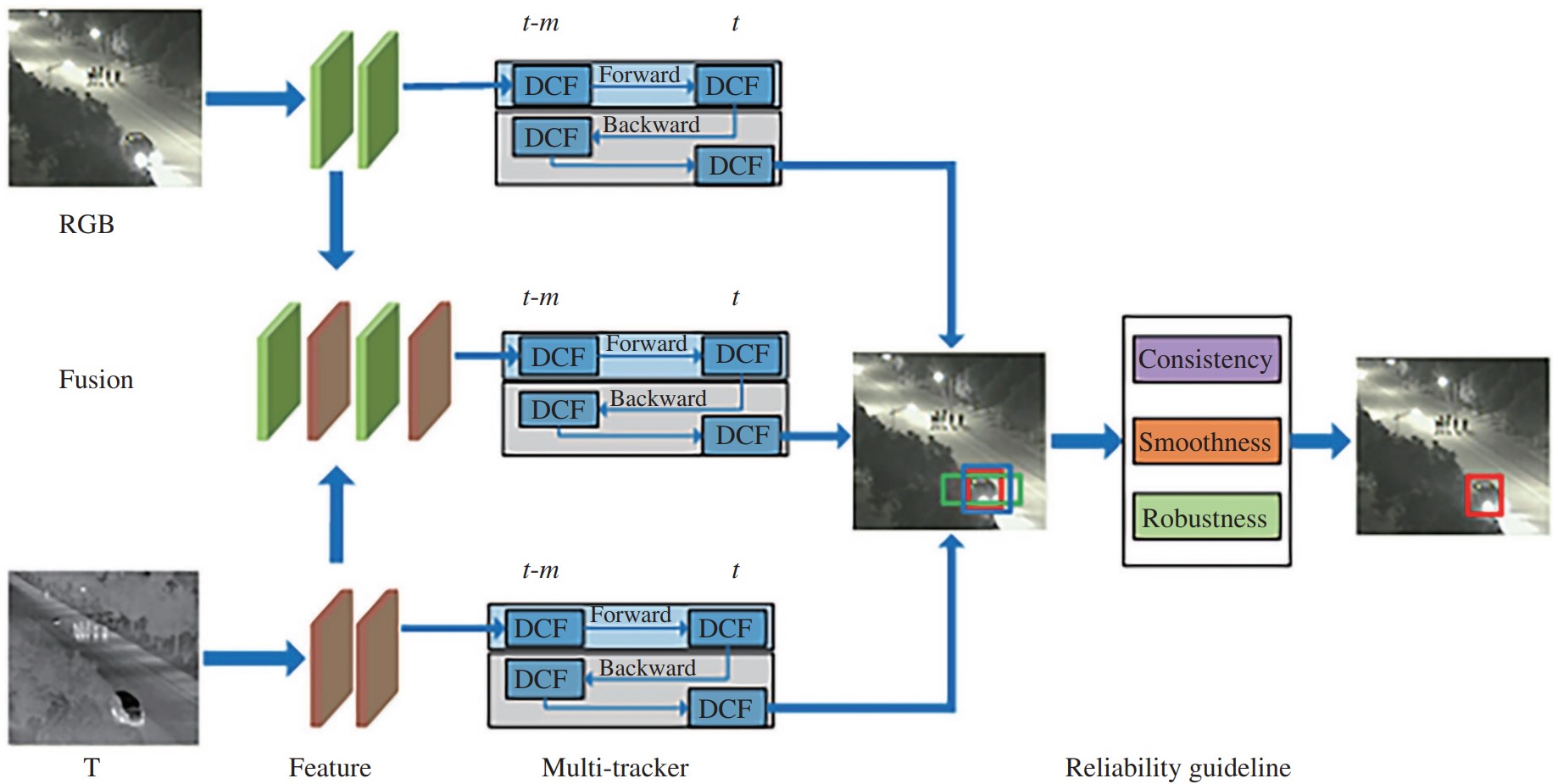
论文来源: RGBT tracking via reliable feature configuration
许多模型对自适应融合的理解还停留在权重阶段, 大量算力被消耗于权重计算, 同时这种方法并没考虑到低可靠性模态对另一模态的影响. 本文作者将提出新颖的基于可靠性的特征配置方法, 实现鲁棒性 RGBT 追踪. 其将使用 3 种追踪器来跟踪目标, 使用特殊的评分机制来评估追踪器可靠性, 并选取得分最高的结果作为输出.
首先, 来自可见光, 热红外的特征配置以及它们的融合特征配置被输入到基于 DCF 滤波器的跟踪器中. 特征配置的计算方式如下:
X = X h ⊕ X c X = X_h \oplus X_c X = X h ⊕ X c
其中 ⊕ \oplus ⊕ X h X_h X h X c X_c X c X X X
融合特征配置是两个模态的特征配置的融合, 由于 CN 特征在热红外模态中作用较低, 为平衡两个模态的特征比例, 需要调节它们的权重:
X F = ( X h R ⊕ X h T ) ⊕ ( ( 1 − σ ) X c R ⊕ σ X c T ) X^F = \left(X_h^R \oplus X_h^T \right) \oplus \left((1-\sigma)X_c^R \oplus \sigma X_c^T \right) X F = ( X h R ⊕ X h T ) ⊕ ( ( 1 − σ ) X c R ⊕ σ X c T )
为了提高模型准确度, 作者设计了 3 个跟踪器, 通过一致性、平滑性、鲁棒性来评价 3 个跟踪器, 最终选出最强大的跟踪器.
一致性 :
S c o n s ( t ) k = ∑ j = 0 J w j 1 N ∑ n = 1 N M ( n , [ t − ( J − j ) + 1 ] ) k ∑ j = 0 J w j O ( n , [ t − ( J − j ) + 1 ] ) k + μ ∑ j = 0 J w j \large S_{cons(t)}^k = \frac { \sum\limits_{j=0}^J w_j \frac 1N \sum\limits_{n=1}^N M_{(n, [t-(J-j)+1])}^k } { \sum\limits_{j=0}^J w_j O_{(n, [t-(J-j)+1])}^k + \mu \sum\limits_{j=0}^J w_j } S c o n s ( t ) k = j = 0 ∑ J w j O ( n , [ t − ( J − j ) + 1 ] ) k + μ j = 0 ∑ J w j j = 0 ∑ J w j N 1 n = 1 ∑ N M ( n , [ t − ( J − j ) + 1 ] ) k
其中 N N N t t t J J J M ( n , [ t − ( J − j ) + 1 ] ) k M_{(n, [t-(J-j)+1])}^k M ( n , [ t − ( J − j ) + 1 ] ) k O ( n , [ t − ( J − j ) + 1 ] ) k O_{(n, [t-(J-j)+1])}^k O ( n , [ t − ( J − j ) + 1 ] ) k [ t − ( J − j ) + 1 ] [t-(J-j)+1] [ t − ( J − j ) + 1 ] k k k n n n w j = ( 1.1 ) j w_j = (1.1)^j w j = ( 1 . 1 ) j ( j + 1 ) (j+1) ( j + 1 ) S c o n s ( t ) k S_{cons(t)}^k S c o n s ( t ) k k k k t t t μ \mu μ
平滑性 :
S s m o o ( t ) k = ∑ j = 0 J w j exp ( − 2 ∣ ∣ B t − ( J − j ) k − B t − ( J − j ) + 1 k ∣ ∣ 2 ( W t − ( J − j ) + 1 k + H t − ( J − j ) + 1 k ) 2 ) ∑ j = 0 J w j \large S_{smoo(t)}^k = \frac { \sum\limits_{j=0}^J w_j \exp \left( -\frac{2|| B_{t-(J-j)}^k - B_{t-(J-j)+1}^k ||^2}{(W_{t-(J-j)+1}^k + H_{t-(J-j)+1}^k)^2} \right) } { \sum\limits_{j=0}^J w_j } S s m o o ( t ) k = j = 0 ∑ J w j j = 0 ∑ J w j exp ( − ( W t − ( J − j ) + 1 k + H t − ( J − j ) + 1 k ) 2 2 ∣ ∣ B t − ( J − j ) k − B t − ( J − j ) + 1 k ∣ ∣ 2 )
其中 B t − ( J − j ) k B_{t-(J-j)}^k B t − ( J − j ) k t − ( J − j ) t-(J-j) t − ( J − j ) k k k W , H W, H W , H B B B
鲁棒性 :
S r o b ( t ) k = exp ( − ∣ ∣ B → t k − B ← t k ∣ ∣ 2 δ 2 ) S_{rob(t)}^k = \exp(-\frac{|| \overrightarrow B_t^k - \overleftarrow B_t^k ||^2}{\delta^2}) S r o b ( t ) k = exp ( − δ 2 ∣ ∣ B t k − B t k ∣ ∣ 2 )
其中 B → t k \overrightarrow B_t^k B t k t t t k k k 1 1 1
最终得分如下:
S r e l k = ξ S c o n s ( t ) k + ( 1 − ξ ) S s m o o ( t ) k + γ S r o b ( t ) k S_{rel}^k = \xi S_{cons(t)}^k + (1-\xi) S_{smoo(t)}^k + \gamma S_{rob(t)}^k S r e l k = ξ S c o n s ( t ) k + ( 1 − ξ ) S s m o o ( t ) k + γ S r o b ( t ) k
其中 ξ \xi ξ γ \gamma γ
该模型的缺点注意有两处:
反向追踪计算量大, 作者将在之后尝试多线程等方法来加速计算. 增加特征数量并未提高模型精度, 作者将尝试其它更具辨别力的特征进行实验.