Denoising Diffusion Probabilistic Models
论文作者为Jonathan Ho , 于2020年发布于NeurIPS , 与ICML, ICLR并称为机器学习三大顶会. 本论文是将扩散算法用于图像生成的开山之作.
设某个系统在 t t t X t X_t X t P = { X t , X t − 1 , … , X 0 } P = \{X_t, X_{t-1}, \dots, X_0\} P = { X t , X t − 1 , … , X 0 }
P ( X i ∣ X i − 1 , X i − 2 , ⋯ , X 0 ) = P ( X i ∣ X i − 1 ) (1-1) P(X_i | X_{i-1}, X_{i-2}, \cdots, X_0) = P(X_i | X_{i-1}) \tag{1-1} P ( X i ∣ X i − 1 , X i − 2 , ⋯ , X 0 ) = P ( X i ∣ X i − 1 ) ( 1 - 1 )
则称其为马尔可夫链
已知 z ∼ N ( z ; μ , σ 2 I ) z \sim \mathcal{N}(z; \mu, \sigma^2 \bm{I}) z ∼ N ( z ; μ , σ 2 I ) z z z μ \mu μ σ 2 \sigma^2 σ 2 ϵ \epsilon ϵ
z = μ + σ ⋅ ϵ , ϵ ∼ N ( 0 , I ) (1-2) z = \mu + \sigma \cdot \epsilon, \epsilon \sim \mathcal{N}(0, \bm{I}) \tag{1-2} z = μ + σ ⋅ ϵ , ϵ ∼ N ( 0 , I ) ( 1 - 2 )
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) (1-3) P(A | B) = \frac{P(B | A) \cdot P(A)}{P(B)} \tag{1-3} P ( A ∣ B ) = P ( B ) P ( B ∣ A ) ⋅ P ( A ) ( 1 - 3 )
在给定条件 C C C
P ( A ∣ B , C ) = P ( B ∣ A , C ) ⋅ P ( A ∣ C ) P ( B ∣ C ) (1-4) P(A | B, C) = \frac{P(B | A, C) \cdot P(A | C)}{P(B | C)} \tag{1-4} P ( A ∣ B , C ) = P ( B ∣ C ) P ( B ∣ A , C ) ⋅ P ( A ∣ C ) ( 1 - 4 )
证明如下:
P ( A ∣ B , C ) = P ( B , C ∣ A ) ⋅ P ( A ) P ( B , C ) = P ( B ∣ A , C ) ⋅ P ( C ∣ A ) ⋅ P ( A ) P ( B , C ) = P ( B ∣ A , C ) ⋅ P ( A ∣ C ) ⋅ P ( C ) P ( B , C ) = P ( B ∣ A , C ) ⋅ P ( A ∣ C ) P ( B ∣ C ) \large \begin{array}{ll} & P(A|B,C) \\\\ =& \frac{P(B,C|A) \cdot P(A)}{P(B,C)} \\\\ =& \frac{P(B|A,C) \cdot P(C|A) \cdot P(A)}{P(B,C)} \\\\ =& \frac{P(B|A,C) \cdot P(A|C) \cdot P(C)}{P(B,C)} \\\\ =& \frac{P(B|A,C) \cdot P(A|C)}{P(B|C)} \end{array} = = = = P ( A ∣ B , C ) P ( B , C ) P ( B , C ∣ A ) ⋅ P ( A ) P ( B , C ) P ( B ∣ A , C ) ⋅ P ( C ∣ A ) ⋅ P ( A ) P ( B , C ) P ( B ∣ A , C ) ⋅ P ( A ∣ C ) ⋅ P ( C ) P ( B ∣ C ) P ( B ∣ A , C ) ⋅ P ( A ∣ C )
若 X ∼ N ( μ , σ 2 ) X \sim \mathcal{N}(\mu, \sigma^2) X ∼ N ( μ , σ 2 )
f ( x ) = 1 2 π σ 2 exp ( − 1 2 ( x − μ ) 2 σ 2 ) (1-5) f(x) = \frac{1}{\sqrt{2 \pi}\sigma^2} \exp(-\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2}) \tag{1-5} f ( x ) = 2 π σ 2 1 exp ( − 2 1 σ 2 ( x − μ ) 2 ) ( 1 - 5 )
可以发现前面的系数只与方差 σ 2 \sigma^2 σ 2
f ( x ) ∝ exp ( − 1 2 ( x − μ ) 2 σ 2 ) (1-6) f(x) \propto \exp(-\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2}) \tag{1-6} f ( x ) ∝ exp ( − 2 1 σ 2 ( x − μ ) 2 ) ( 1 - 6 )
已有数据分布 x 0 ∼ q ( x 0 ) x_0 \sim q(x_0) x 0 ∼ q ( x 0 ) x 1 x_1 x 1 x 1 x_1 x 1 x 0 x_0 x 0 T T T x T x_T x T
q ( x 1 , ⋯ , x T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) (2-1) q(x_1, \cdots, x_T | x_0) = \prod_{t=1}^T q(x_t | x_{t-1}) \tag{2-1} q ( x 1 , ⋯ , x T ∣ x 0 ) = t = 1 ∏ T q ( x t ∣ x t − 1 ) ( 2 - 1 )
由 x t − 1 x_{t-1} x t − 1 x t x_t x t
q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) (2-2) q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t \bm{I}) \tag{2-2} q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) ( 2 - 2 )
其中 β ∈ ( 0 , 1 ) \beta \in (0, 1) β ∈ ( 0 , 1 )
它还可以写为
x t = α t x t − 1 + β t ϵ t , ϵ t ∼ N ( 0 , I ) , α t = 1 − β t (2-3) x_t = \sqrt{\alpha_t}x_{t-1}+\sqrt{\beta_t}\epsilon_t, \epsilon_t \sim \mathcal{N}(0, \bm{I}), \alpha_t = 1 - \beta_t \tag{2-3} x t = α t x t − 1 + β t ϵ t , ϵ t ∼ N ( 0 , I ) , α t = 1 − β t ( 2 - 3 )
使用该方法重复计算, 最终可以得到 x t x_t x t x 0 x_0 x 0 x t x_t x t
对 x t − 1 x_{t-1} x t − 1
x t = α t x t − 1 + β t ϵ t = α t ( α t − 1 x t − 2 + β t − 1 ϵ t − 1 ) + β t ϵ t = ⋯ = x 0 ∏ i = 1 t α i + α t α t − 1 ⋯ α 2 β 1 ϵ 1 + α t α t − 1 ⋯ α 3 β 2 ϵ 2 + ⋯ + α t β t − 1 ϵ t − 1 + β t ϵ t (2-4) \begin{array}{ll} x_t &= \sqrt{\alpha_t}x_{t-1}+\sqrt{\beta_t}\epsilon_t \\ &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{\beta_{t-1}}\epsilon_{t-1}) + \sqrt{\beta_t}\epsilon_t \\ &= \cdots \\ &= x_0 \prod_{i=1}^t \sqrt{\alpha_i} + \sqrt{\alpha_t \alpha_{t-1} \cdots \alpha_{2} \beta_1 } \epsilon_1 + \sqrt{\alpha_t \alpha_{t-1} \cdots \alpha_{3} \beta_2 } \epsilon_2 + \cdots + \sqrt{\alpha_t \beta_{t-1}} \epsilon_{t-1} + \sqrt{\beta_t} \epsilon_t \\ \end{array} \tag{2-4} x t = α t x t − 1 + β t ϵ t = α t ( α t − 1 x t − 2 + β t − 1 ϵ t − 1 ) + β t ϵ t = ⋯ = x 0 ∏ i = 1 t α i + α t α t − 1 ⋯ α 2 β 1 ϵ 1 + α t α t − 1 ⋯ α 3 β 2 ϵ 2 + ⋯ + α t β t − 1 ϵ t − 1 + β t ϵ t ( 2 - 4 )
由于 ϵ i ∼ N ( 0 , I ) \epsilon_i \sim \mathcal{N}(0, \bm{I}) ϵ i ∼ N ( 0 , I )
例如:
α t α t − 1 ⋯ α 2 β 1 ϵ 1 ∼ N ( 0 , α t α t − 1 ⋯ α 2 β 1 I ) (2-5) \sqrt{\alpha_t \alpha_{t-1} \cdots \alpha_{2} \beta_1 } \epsilon_1 \sim \mathcal{N}(0, \alpha_t \alpha_{t-1} \cdots \alpha_{2} \beta_1 \bm{I}) \tag{2-5} α t α t − 1 ⋯ α 2 β 1 ϵ 1 ∼ N ( 0 , α t α t − 1 ⋯ α 2 β 1 I ) ( 2 - 5 )
所以
N ( 0 , α t α t − 1 ⋯ α 2 β 1 I ) + N ( 0 , α t α t − 1 ⋯ α 3 β 2 I ) + ⋯ + N ( 0 , α t β t − 1 I ) + N ( 0 , β t I ) = N { 0 , α t α t − 1 ⋯ α 2 ( 1 − α 1 ) I } + N { 0 , α t α t − 1 ⋯ α 3 ( 1 − α 2 ) I } + ⋯ + N { 0 , α t ( 1 − α t − 1 ) I } + N { 0 , ( 1 − α t ) I } = N { 0 , ( ∏ i = 2 t α i − ∏ i = 1 t α i + ∏ i = 3 t α i − ∏ i = 2 t α i + ⋯ + 1 − α t ) I } = N ( 0 , 1 − ∏ i = 1 t α i I ) = N { 0 , ( 1 − α ˉ ) I } , α ˉ = α 1 α 2 ⋯ α t (2-6) \begin{array}{ll} & \mathcal{N}(0, \alpha_t \alpha_{t-1} \cdots \alpha_{2} \beta_1 \bm{I}) + \mathcal{N}(0, \alpha_t \alpha_{t-1} \cdots \alpha_{3} \beta_2 \bm{I}) + \cdots + \mathcal{N}(0, \alpha_t \beta_{t-1} \bm{I}) + \mathcal{N}(0, \beta_t \bm{I}) \\\\ =& \mathcal{N}\{0, \alpha_t \alpha_{t-1} \cdots \alpha_{2} (1-\alpha_1) \bm{I}\} + \mathcal{N}\{0, \alpha_t \alpha_{t-1} \cdots \alpha_{3} (1-\alpha_2) \bm{I}\} + \cdots + \mathcal{N}\{0, \alpha_t (1-\alpha_{t-1}) \bm{I}\} + \mathcal{N}\{0, (1-\alpha_t) \bm{I}\} \\\\ =& \mathcal{N}\{0, (\prod_{i=2}^t \alpha_i - \prod_{i=1}^t \alpha_i + \prod_{i=3}^t \alpha_i - \prod_{i=2}^t \alpha_i + \cdots + 1 - \alpha_t)\bm{I}\} \\\\ =& \mathcal{N}(0, 1 - \prod_{i=1}^t \alpha_i \bm{I}) \\\\ =& \mathcal{N}\{0, (1 - \bar{\alpha}) \bm{I}\}, \bar{\alpha} = \alpha_1 \alpha_2 \cdots \alpha_t \\\\ \end{array} \tag{2-6} = = = = N ( 0 , α t α t − 1 ⋯ α 2 β 1 I ) + N ( 0 , α t α t − 1 ⋯ α 3 β 2 I ) + ⋯ + N ( 0 , α t β t − 1 I ) + N ( 0 , β t I ) N { 0 , α t α t − 1 ⋯ α 2 ( 1 − α 1 ) I } + N { 0 , α t α t − 1 ⋯ α 3 ( 1 − α 2 ) I } + ⋯ + N { 0 , α t ( 1 − α t − 1 ) I } + N { 0 , ( 1 − α t ) I } N { 0 , ( ∏ i = 2 t α i − ∏ i = 1 t α i + ∏ i = 3 t α i − ∏ i = 2 t α i + ⋯ + 1 − α t ) I } N ( 0 , 1 − ∏ i = 1 t α i I ) N { 0 , ( 1 − α ˉ ) I } , α ˉ = α 1 α 2 ⋯ α t ( 2 - 6 )
因此
p ( x t ∣ x 0 ) = α ˉ x 0 + 1 − α ˉ ϵ = N ( x t ; α ˉ x 0 , ( 1 − α ˉ ) I ) , ϵ ∼ N ( 0 , I ) (2-7) p(x_t | x_0) = \sqrt{\bar{\alpha}} x_0 + \sqrt{1 - \bar{\alpha}} \epsilon = \mathcal{N}(x_t; \sqrt{\bar{\alpha}} x_0, (1-\bar{\alpha}) \bm{I}) , \epsilon \sim \mathcal{N}(0, \bm{I}) \tag{2-7} p ( x t ∣ x 0 ) = α ˉ x 0 + 1 − α ˉ ϵ = N ( x t ; α ˉ x 0 , ( 1 − α ˉ ) I ) , ϵ ∼ N ( 0 , I ) ( 2 - 7 )
也就是说, 只需要一步就可以由 x 0 x_0 x 0 x t x_t x t
由肉眼看来, 从 x 0 x_0 x 0 x t x_t x t
当步数 t t t β t < 1 \beta_t < 1 β t < 1 t t t
lim n → ∞ α ˉ = 0 (2-8) \lim_{n \rightarrow \infty} \bar{\alpha} = 0 \tag{2-8} n → ∞ lim α ˉ = 0 ( 2 - 8 )
而通过上面的计算, 我们得知
p ( x t ∣ x 0 ) = N ( x t ; α ˉ x 0 , ( 1 − α ˉ ) I ) (2-9) p(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}} x_0, (1-\bar{\alpha}) \bm{I}) \tag{2-9} p ( x t ∣ x 0 ) = N ( x t ; α ˉ x 0 , ( 1 − α ˉ ) I ) ( 2 - 9 )
所以
lim t → ∞ q ( x t ∣ x 0 ) = N ( 0 , I ) , lim t → ∞ p ( x t ) = N ( 0 , I ) (2-10) \lim_{t \rightarrow \infty} q(x_t | x_0) = \mathcal{N}(0, \bm{I}), \lim_{t \rightarrow \infty} p(x_t) = \mathcal{N}(0, \bm{I}) \tag{2-10} t → ∞ lim q ( x t ∣ x 0 ) = N ( 0 , I ) , t → ∞ lim p ( x t ) = N ( 0 , I ) ( 2 - 1 0 )
通过上面的过程, 我们有了逐步杂乱化的数据分布 x t x_t x t x t − 1 x_{t-1} x t − 1 x t x_t x t q θ ( x t − 1 ∣ x t ) q_\theta(x_{t-1} | x_t) q θ ( x t − 1 ∣ x t ) θ \theta θ
根据贝叶斯公式, 有
p ( x t − 1 ∣ x t ) = p ( x t ∣ x t − 1 ) ⋅ p ( x t − 1 ) p ( x t ) (3-1) p(x_{t-1} | x_t) = \frac{p(x_t | x_{t-1}) \cdot p(x_{t-1})}{p(x_t)} \tag{3-1} p ( x t − 1 ∣ x t ) = p ( x t ) p ( x t ∣ x t − 1 ) ⋅ p ( x t − 1 ) ( 3 - 1 )
但 p ( x t − 1 ) p(x_{t-1}) p ( x t − 1 ) p ( x t ) p(x_t) p ( x t ) x 0 x_0 x 0
p ( x t − 1 ∣ x t , x 0 ) = p ( x t ∣ x t − 1 , x 0 ) ⋅ p ( x t − 1 ∣ x 0 ) p ( x t ∣ x 0 ) (3-2) p(x_{t-1} | x_t, x_0) = \frac{p(x_t | x_{t-1}, x_0) \cdot p(x_{t-1} | x_0)}{p(x_t | x_0)} \tag{3-2} p ( x t − 1 ∣ x t , x 0 ) = p ( x t ∣ x 0 ) p ( x t ∣ x t − 1 , x 0 ) ⋅ p ( x t − 1 ∣ x 0 ) ( 3 - 2 )
根据马尔可夫链的性质, 我们知道下一状态只与上一状态有关, 所以 p ( x t ∣ x t − 1 , x 0 ) = p ( x t ∣ x t − 1 ) p(x_t | x_{t-1}, x_0) = p(x_t | x_{t-1}) p ( x t ∣ x t − 1 , x 0 ) = p ( x t ∣ x t − 1 )
p ( x t − 1 ∣ x t , x 0 ) = p ( x t ∣ x t − 1 ) ⋅ p ( x t − 1 ∣ x 0 ) p ( x t ∣ x 0 ) (3-3) p(x_{t-1} | x_t, x_0) = \frac{p(x_t | x_{t-1}) \cdot p(x_{t-1} | x_0)}{p(x_t | x_0)} \tag{3-3} p ( x t − 1 ∣ x t , x 0 ) = p ( x t ∣ x 0 ) p ( x t ∣ x t − 1 ) ⋅ p ( x t − 1 ∣ x 0 ) ( 3 - 3 )
根据公式 ( 2 − 1 ) (2-1) ( 2 − 1 ) ( 2 − 2 ) (2-2) ( 2 − 2 )
1. p ( x t ∣ x t − 1 ) ∼ N ( α t x t − 1 , ( 1 − α t ) I ) 2. p ( x t − 1 ∣ x 0 ) ∼ N ( α ˉ t − 1 x 0 , ( 1 − α ˉ t − 1 ) I ) 3. p ( x t ∣ x 0 ) ∼ N ( α ˉ t x 0 , ( 1 − α ˉ t ) I ) (3-4) \large \begin{array}{ll} 1. p(x_t | x_{t-1}) &\sim \mathcal{N}(\sqrt{\alpha_t}x_{t-1}, (1 - \alpha_t)\bm{I}) \\ 2. p(x_{t-1} | x_0) &\sim \mathcal{N}(\sqrt{\bar{\alpha}_{t-1}}x_0, (1 - \bar{\alpha}_{t-1})\bm{I}) \\ 3. p(x_t | x_0) &\sim \mathcal{N}(\sqrt{\bar{\alpha}_t}x_0, (1 - \bar{\alpha}_t)\bm{I}) \end{array} \tag{3-4} 1 . p ( x t ∣ x t − 1 ) 2 . p ( x t − 1 ∣ x 0 ) 3 . p ( x t ∣ x 0 ) ∼ N ( α t x t − 1 , ( 1 − α t ) I ) ∼ N ( α ˉ t − 1 x 0 , ( 1 − α ˉ t − 1 ) I ) ∼ N ( α ˉ t x 0 , ( 1 − α ˉ t ) I ) ( 3 - 4 )
注意第一个不是 α ˉ t \bar{\alpha}_t α ˉ t α t \alpha_t α t α ˉ t = α 1 α 2 ⋯ α t \bar{\alpha}_t = \alpha_1 \alpha_2 \cdots \alpha_t α ˉ t = α 1 α 2 ⋯ α t x t − 1 x_{t-1} x t − 1 x t x_t x t
可以发现, 以上三项全部都是正态分布, 其中方差均为超参数, 是人为指定的常数, 即正态分布的系数也是预先确定的常数, 所以我们不关心系数具体是什么, 因而有
p ( x t − 1 ∣ x t , x 0 ) ∝ exp { − 1 2 [ ( x t − α t x t − 1 ) 2 β t + ( x t − 1 − α ˉ t − 1 x 0 ) 2 1 − α ˉ t − 1 − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ] } = exp [ − 1 2 ( x t 2 β t − 2 α t x t x t − 1 β t + α t x t − 1 2 β t + x t − 1 2 1 − α ˉ t − 1 − 2 α ˉ t − 1 x 0 x t − 1 1 − α ˉ t − 1 + α ˉ t − 1 x 0 2 1 − α ˉ t − 1 − x t 2 1 − α ˉ t + 2 α ˉ t x 0 x t 1 − α ˉ t − α ˉ t x 0 2 1 − α ˉ t ) ] = exp { − 1 2 [ ( α t β t + 1 1 − α ˉ t − 1 ) x t − 1 2 − ( 2 α t β t x t + 2 α ˉ t − 1 1 − α ˉ t − 1 x 0 ) x t − 1 + C ( x 0 , x t ) ] } (3-5) \Large \begin{array}{ll} & p(x_{t-1} | x_t, x_0) \\\\ \propto & \exp{\left\{ -\frac12 \left[ \frac{(x_t - \sqrt{\alpha_t}x_{t-1})^2}{\beta_t} + \frac{(x_{t-1} - \sqrt{\bar{\alpha}_{t-1}}x_0)^2}{1-\bar{\alpha}_{t-1}} - \frac{(x_t - \sqrt{\bar{\alpha}_t}x_0)^2}{1-\bar{\alpha}_t} \right]\right\}} \\\\ = & \exp{\left[ -\frac12 \left( \frac{x_t^2}{\beta_t} - \frac{2\sqrt{\alpha_t}x_t x_{t-1}}{\beta_t} + \frac{\alpha_t x_{t-1}^2}{\beta_t} + \frac{x_{t-1}^2}{1-\bar{\alpha}_{t-1}}\right. \right.} - \frac{2\sqrt{\bar{\alpha}_{t-1}}x_0 x_{t-1}}{1-\bar{\alpha}_{t-1}} \\\\ & \left.\left. + \frac{\bar{\alpha}_{t-1} x_0^2}{1-\bar{\alpha}_{t-1}} - \frac{x_t^2}{1-\bar{\alpha}_t} + \frac{2\sqrt{\bar{\alpha}_t}x_0 x_t}{1-\bar{\alpha}_t} - \frac{\bar{\alpha}_t x_0^2}{1-\bar{\alpha}_t} \right)\right] \\\\ =& \exp{\left\{ -\frac12 \left[ \left(\frac{\alpha_t}{\beta_t} + \frac1{1-\bar{\alpha}_{t-1}}\right)x_{t-1}^2 - \left(\frac{2\sqrt{\alpha_t}}{\beta_t}x_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}x_0\right)x_{t-1} + C(x_0, x_t) \right]\right\}} \end{array} \tag{3-5} ∝ = = p ( x t − 1 ∣ x t , x 0 ) exp { − 2 1 [ β t ( x t − α t x t − 1 ) 2 + 1 − α ˉ t − 1 ( x t − 1 − α ˉ t − 1 x 0 ) 2 − 1 − α ˉ t ( x t − α ˉ t x 0 ) 2 ] } exp [ − 2 1 ( β t x t 2 − β t 2 α t x t x t − 1 + β t α t x t − 1 2 + 1 − α ˉ t − 1 x t − 1 2 − 1 − α ˉ t − 1 2 α ˉ t − 1 x 0 x t − 1 + 1 − α ˉ t − 1 α ˉ t − 1 x 0 2 − 1 − α ˉ t x t 2 + 1 − α ˉ t 2 α ˉ t x 0 x t − 1 − α ˉ t α ˉ t x 0 2 ) ] exp { − 2 1 [ ( β t α t + 1 − α ˉ t − 1 1 ) x t − 1 2 − ( β t 2 α t x t + 1 − α ˉ t − 1 2 α ˉ t − 1 x 0 ) x t − 1 + C ( x 0 , x t ) ] } ( 3 - 5 )
其中 C ( x 0 , x t ) C(x_0, x_t) C ( x 0 , x t ) x 0 , x t x_0, x_t x 0 , x t
我们知道正态分布化开后是
exp { − ( x − μ ) 2 2 σ 2 } = exp { − 1 2 ( 1 σ 2 x 2 − 2 μ σ 2 x + μ 2 σ 2 ) } (3-6) \exp\left\{-\frac{(x-\mu)^2}{2\sigma^2}\right\} = \exp\left\{-\frac12 \left( \frac1{\sigma^2}x^2 - \frac{2\mu}{\sigma^2}x + \frac{\mu^2}{\sigma^2} \right) \right\} \tag{3-6} exp { − 2 σ 2 ( x − μ ) 2 } = exp { − 2 1 ( σ 2 1 x 2 − σ 2 2 μ x + σ 2 μ 2 ) } ( 3 - 6 )
与上面得到的结果仔细比对
exp { − 1 2 [ ( α t β t + 1 1 − α ˉ t − 1 ) x t − 1 2 − ( 2 α t β t x t + 2 α ˉ t − 1 1 − α ˉ t − 1 x 0 ) x t − 1 + C ( x 0 , x t ) ] } exp { − 1 2 [ 1 σ 2 x 2 − 2 μ σ 2 x + μ 2 σ 2 ] } (3-7) \large \begin{array}{ll} \exp\left\{ -\frac12 \left[ \left(\frac{\alpha_t}{\beta_t} + \frac1{1-\bar{\alpha}_{t-1}}\right) x_{t-1}^2 - \left(\frac{2\sqrt{\alpha_t}}{\beta_t}x_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}}x_0\right)x_{t-1} + C(x_0, x_t) \right]\right\} \\\\ \exp\left\{-\frac12 \left[ \frac1{\sigma^2} x^2 - \frac{2\mu}{\sigma^2}x + \frac{\mu^2}{\sigma^2} \right] \right\} \end{array} \tag{3-7} exp { − 2 1 [ ( β t α t + 1 − α ˉ t − 1 1 ) x t − 1 2 − ( β t 2 α t x t + 1 − α ˉ t − 1 2 α ˉ t − 1 x 0 ) x t − 1 + C ( x 0 , x t ) ] } exp { − 2 1 [ σ 2 1 x 2 − σ 2 2 μ x + σ 2 μ 2 ] } ( 3 - 7 )
可以发现上下各项都可以一一对应, 即 p ( x t − 1 ∣ x t , x 0 ) p(x_{t-1} | x_t, x_0) p ( x t − 1 ∣ x t , x 0 )
σ ~ 2 = β t ( 1 − α ˉ t − 1 ) α t − α t α ˉ t − 1 + β t = β t ( 1 − α ˉ t − 1 ) 1 − α ˉ t μ ~ = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + β t α ˉ t − 1 1 − α ˉ t x 0 (3-8) \Large \begin{array}{ll} \tilde\sigma^2 &= \frac{\beta_t (1-\bar{\alpha}_{t-1})}{\alpha_t - \alpha_t \bar{\alpha}_{t-1} + \beta_t} = \frac{\beta_t (1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} \\\\ \tilde\mu &= \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}x_t + \frac{\beta_t \sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_t}x_0 \end{array} \tag{3-8} σ ~ 2 μ ~ = α t − α t α ˉ t − 1 + β t β t ( 1 − α ˉ t − 1 ) = 1 − α ˉ t β t ( 1 − α ˉ t − 1 ) = 1 − α ˉ t α t ( 1 − α ˉ t − 1 ) x t + 1 − α ˉ t β t α ˉ t − 1 x 0 ( 3 - 8 )
根据公式 ( 2 − 7 ) (2-7) ( 2 − 7 )
x 0 = 1 α ˉ t ( x t − 1 − α ˉ t ϵ t ) (3-9) x_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}\left( x_t - \sqrt{1-\bar{\alpha}_t}\epsilon_t \right) \tag{3-9} x 0 = α ˉ t 1 ( x t − 1 − α ˉ t ϵ t ) ( 3 - 9 )
代入公式 ( 3 − 8 ) (3-8) ( 3 − 8 )
μ ~ = [ α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t + β t α ˉ t − 1 ( 1 − α ˉ t ) α ˉ t ] x t − β t α ˉ t − 1 1 − α ˉ t ( 1 − α ˉ t ) α ˉ t ϵ t = α t ⋅ α ˉ t ( 1 − α ˉ t − 1 ) + β t α ˉ t − 1 ( 1 − α ˉ t ) α ˉ t x t − β t 1 − α ˉ t ( 1 − α ˉ t ) ⋅ α t ϵ t = α t ⋅ α ˉ t − 1 ( 1 − α ˉ t − 1 ) + β t α ˉ t − 1 ( 1 − α ˉ t ) α ˉ t x t − β t 1 − α ˉ t ⋅ α t ϵ t = α ˉ t − 1 ( α t − α ˉ t + β t ) ( 1 − α ˉ t ) α ˉ t x t − β t 1 − α ˉ t ⋅ α t ϵ t = 1 α t ( x t − β t 1 − α ˉ t ϵ t ) (3-10) \Large \begin{array}{ll} \tilde\mu &= \left[ \frac{\sqrt{\alpha_t}(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t} + \frac{\beta_t \sqrt{\bar{\alpha}_{t-1}}}{(1-\bar{\alpha}_t) \sqrt{\bar{\alpha}_t}} \right] x_t - \frac{\beta_t \sqrt{\bar{\alpha}_{t-1}}\sqrt{1-\bar{\alpha}_t}}{(1-\bar{\alpha}_t) \sqrt{\bar{\alpha}_t}} \epsilon_t \\\\ &= \frac{\sqrt{\alpha_t} \cdot \sqrt{\bar{\alpha}_t}(1-\bar{\alpha}_{t-1})+\beta_t \sqrt{\bar{\alpha}_{t-1}}}{(1-\bar{\alpha}_t)\sqrt{\bar{\alpha}_t}} x_t - \frac{\beta_t \sqrt{1-\bar{\alpha}_t}}{(1-\bar{\alpha}_t) \cdot \sqrt{\alpha_t}} \epsilon_t \\\\ &= \frac{\alpha_t \cdot \sqrt{\bar{\alpha}_{t-1}} (1-\bar{\alpha}_{t-1}) + \beta_t \sqrt{\bar{\alpha}_{t-1}}}{(1-\bar{\alpha}_t) \sqrt{\bar{\alpha}_t}}x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t} \cdot \sqrt{\alpha_t}} \epsilon_t \\\\ &= \frac{\sqrt{\bar{\alpha}_{t-1}}(\alpha_t - \bar{\alpha}_t + \beta_t)}{(1-\bar{\alpha}_t)\sqrt{\bar{\alpha}_t}} x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t} \cdot \sqrt{\alpha_t}} \epsilon_t \\\\ &= \frac{1}{\sqrt{\alpha}_t}\left( x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_t \right) \end{array} \tag{3-10} μ ~ = [ 1 − α ˉ t α t ( 1 − α ˉ t − 1 ) + ( 1 − α ˉ t ) α ˉ t β t α ˉ t − 1 ] x t − ( 1 − α ˉ t ) α ˉ t β t α ˉ t − 1 1 − α ˉ t ϵ t = ( 1 − α ˉ t ) α ˉ t α t ⋅ α ˉ t ( 1 − α ˉ t − 1 ) + β t α ˉ t − 1 x t − ( 1 − α ˉ t ) ⋅ α t β t 1 − α ˉ t ϵ t = ( 1 − α ˉ t ) α ˉ t α t ⋅ α ˉ t − 1 ( 1 − α ˉ t − 1 ) + β t α ˉ t − 1 x t − 1 − α ˉ t ⋅ α t β t ϵ t = ( 1 − α ˉ t ) α ˉ t α ˉ t − 1 ( α t − α ˉ t + β t ) x t − 1 − α ˉ t ⋅ α t β t ϵ t = α t 1 ( x t − 1 − α ˉ t β t ϵ t ) ( 3 - 1 0 )
最后我们就可以用 x t x_t x t x t − 1 x_{t-1} x t − 1
x t − 1 = μ ~ + σ ~ ϵ = 1 α t ( x t − β t 1 − α ˉ t ϵ t ) + β t ( 1 − α ˉ t − 1 ) 1 − α ˉ t ϵ (3-11) \Large x_{t-1} = \tilde \mu + \tilde \sigma \epsilon = \frac{1}{\sqrt{\alpha}_t}\left( x_t - \frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_t \right) + \sqrt{\frac{\beta_t (1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}} \epsilon \tag{3-11} x t − 1 = μ ~ + σ ~ ϵ = α t 1 ⎝ ⎛ x t − 1 − α ˉ t β t ϵ t ⎠ ⎞ + 1 − α ˉ t β t ( 1 − α ˉ t − 1 ) ϵ ( 3 - 1 1 )
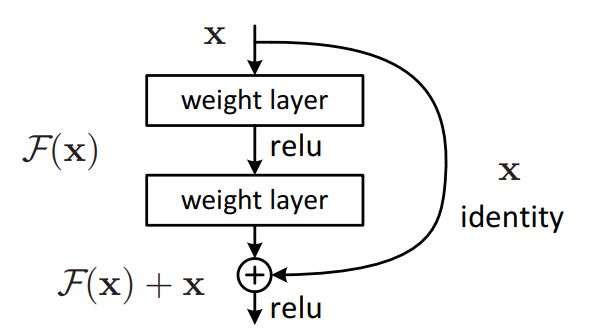
多层神经网络会出现梯度消失和梯度爆炸现象, 其准确度甚至无法达到层数更少的神经网络. 实际上, 由数据处理不等式(DPI)可得, 信息在多层网络直接传播的过程中, 下一层所包含的信息总是小于上一层. 论文Deep Residual Learning for Image Recognition 提出, 使用 Y = X + F ( X , W ) Y = X + F(X, W) Y = X + F ( X , W ) Y = F ( X ) Y = F(X) Y = F ( X )
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 class ResNet (nn.Module): def __init__ (self, channel_input: int , channel_output: int , channel_time: int , device: str = 'cpu' ): """ :param channel_input: 输入通道数 :param channel_output: 输出通道数 :param channel_time: 时间通道数 """ super ().__init__() self.conv1 = nn.Sequential( nn.GroupNorm(32 , channel_input, device=device), nn.SiLU(), nn.Conv2d(channel_input, channel_output, kernel_size=3 , padding=1 ) ) self.time_embedding = nn.Sequential( nn.SiLU(), nn.Linear(channel_time, channel_output) ) self.conv2 = nn.Sequential( nn.GroupNorm(32 , channel_output, device=device), nn.SiLU(), nn.Conv2d(channel_output, channel_output, kernel_size=3 , padding=1 ) ) if channel_input == channel_output: self.shortcut = nn.Identity() else : self.shortcut = nn.Conv2d(channel_input, channel_output, kernel_size=1 ) self.to(device) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: """ :param x: [batch_size, channel_input, h, w] :param t: [batch_size, channel_time] :return: [batch_size, channel_output, h, w] """ result = self.conv1(x) result += self.time_embedding(t)[:, :, None , None ] result = self.conv2(result) return result + self.shortcut(x)
一般的注意力机制公式如下:
o u t = s o f t m a x ( Q K ⊤ d k ) V ⊤ out = softmax(\frac{QK^\top}{\sqrt{d_k}})V^\top o u t = s o f t m a x ( d k Q K ⊤ ) V ⊤
其中 Q , K , V Q, K, V Q , K , V
现已有原图 X ∈ R C × H × W X \in \mathbb{R}^{C \times H \times W} X ∈ R C × H × W X ′ ∈ R C × ( H × W ) X' \in \mathbb{R}^{C \times (H \times W)} X ′ ∈ R C × ( H × W )
通过卷积的方法, 可以将其转化为三个矩阵
Q , K ∈ R C / r × ( H × W ) V ∈ R C × ( H × W ) Q, K \in \mathbb{R}^{C / r \times (H \times W)} \\ V \in \mathbb{R}^{C \times (H \times W)} Q , K ∈ R C / r × ( H × W ) V ∈ R C × ( H × W )
由于 channel 通道在第一维, 所以整个公式也要转置一下
o u t = V [ s o f t m a x ( Q ⊤ K d k ) ] ⊤ ∈ R C × ( H × W ) out = V \left[softmax \left( \frac{Q^\top K}{\sqrt{d_k}} \right) \right]^\top \in \mathbb{R}^{C \times (H \times W)} o u t = V [ s o f t m a x ( d k Q ⊤ K ) ] ⊤ ∈ R C × ( H × W )
其中 d k d_k d k C C C
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 class AttentionBlock (nn.Module): def __init__ (self, in_channels, device='cpu' ): super ().__init__() self.query_conv = nn.Conv2d(in_channels, in_channels // 8 , kernel_size=1 , bias=False ) self.key_conv = nn.Conv2d(in_channels, in_channels // 8 , kernel_size=1 , bias=False ) self.value_conv = nn.Conv2d(in_channels, in_channels, kernel_size=1 , bias=False ) self.to(device) def forward (self, x, t ): batch_size, channels, height, width = x.shape query = self.query_conv(x).view(batch_size, -1 , height * width).permute(0 , 2 , 1 ) key = self.key_conv(x).view(batch_size, -1 , height * width) value = self.value_conv(x).view(batch_size, -1 , height * width) attention = torch.bmm(query, key) / math.sqrt(key.shape[1 ]) attention = F.softmax(attention, dim=-1 ) out = torch.bmm(value, attention.permute(0 , 2 , 1 )) out = out.view(batch_size, channels, height, width) out = out + x return out
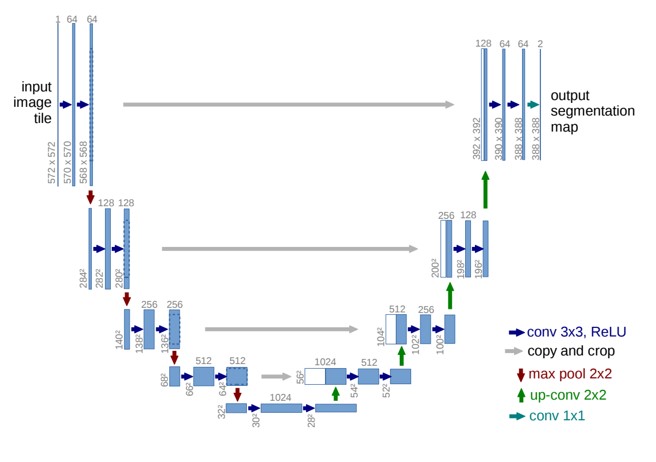
UNet模型不需要过多数学知识, 这里直接给出代码. 但有一点需要注意, 有些模型只有一个输入, 为了便于编码, 全部改为了两个输入, 第二个输入是 timestep, 在部分模型中仅用于占位.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 class DownSample (nn.Module): def __init__ (self, channels: int , device: str = 'cpu' ): super ().__init__() self.op = nn.Conv2d(channels, channels, kernel_size=3 , stride=2 , padding=1 ) self.to(device) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: """ 返回下采样后的图 :param x: [channel, h, w] :param t: 占位 :return: [channel, h, w] """ return self.op(x) class UpSample (nn.Module): def __init__ (self, channels: int , device: str = 'cpu' ): super ().__init__() self.op = nn.Conv2d(channels, channels, kernel_size=3 , padding=1 ) self.to(device) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: """ 返回上采样后的图 :param x: [channel, h, w] :param t: 占位 :return: """ x = F.interpolate(x, scale_factor=2 , mode="nearest" ) x = self.op(x) return x class ModuleList (nn.Module): def __init__ (self, *args ): super ().__init__() self.module_list = [] for idx, module in enumerate (args): self.module_list.append(module) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: for module in self.module_list: x = module(x, t) return x class ModuleAdapter (nn.Module): def __init__ (self, module ): super ().__init__() self.module = module def forward (self, x: torch.Tensor, t: torch.Tensor ): return self.module(x) class UNetModel (nn.Module): def __init__ (self, channel_input: int = 3 , channel_output: int = 3 , channel_model: int = 128 , channel_time: int = 512 , device: str = 'cpu' ): super ().__init__() self.channel_input = channel_input self.channel_output = channel_output self.channel_model = channel_model self.time_embedding = nn.Sequential( nn.Linear(channel_model, channel_time), nn.SiLU(), nn.Linear(channel_time, channel_time) ) self.down_blocks = nn.ModuleList([ ModuleAdapter(nn.Conv2d(3 , 128 , kernel_size=3 , stride=1 , padding=1 )), ResNet(128 , 128 , channel_time, device=device), ResNet(128 , 128 , channel_time, device=device), DownSample(128 , device=device), ModuleList( ResNet(128 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ), ModuleList( ResNet(256 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ), DownSample(256 , device=device), ResNet(256 , 256 , channel_time, device=device), ResNet(256 , 256 , channel_time, device=device), DownSample(256 , device=device), ResNet(256 , 256 , channel_time, device=device), ResNet(256 , 256 , channel_time, device=device), ]) self.up_blocks = nn.ModuleList([ ResNet(512 , 256 , channel_time, device=device), ResNet(512 , 256 , channel_time, device=device), ModuleList( ResNet(512 , 256 , channel_time, device=device), UpSample(256 , device=device), ), ResNet(512 , 256 , channel_time, device=device), ResNet(512 , 256 , channel_time, device=device), ModuleList( ResNet(512 , 256 , channel_time, device=device), UpSample(256 , device=device), ), ModuleList( ResNet(512 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ), ModuleList( ResNet(512 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ), ModuleList( ResNet(384 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), UpSample(256 , device=device), ), ResNet(384 , 128 , channel_time, device=device), ResNet(256 , 128 , channel_time, device=device), ResNet(256 , 128 , channel_time, device=device), ]) self.middle = ModuleList( ResNet(256 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ResNet(256 , 256 , channel_time, device=device), ) self.out = nn.Sequential( nn.GroupNorm(32 , 128 , device=device), nn.SiLU(), nn.Conv2d(128 , 3 , kernel_size=3 , padding=1 ) ) self.to(device) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: """ :param x: :param t: :return: """ emb = self.time_embedding(timestep_embedding(t, self.channel_model)) hs = [] h = x for module in self.down_blocks: h = module(h, emb) hs.append(h) h = self.middle(h, emb) for module in self.up_blocks: temp = torch.cat([h, hs.pop()], dim=1 ) h = module(temp, emb) return self.out(h)
目前这些代码仍有部分问题, 且训练图尺寸与生成图尺寸不同时还会出现图片畸形. 但对初学者来说已足够了解模型思想. 在阅读 DDPM 的构造函数与生成函数时, 建议与上面的公式进行对照, 以方便理解代码含义.
将以下文件放入同一个文件夹中. 先用 Data.py 生成数据集文件, 然后修改 config.yml 里的配置, 最后运行 train.py 即可.
最后, 训练时建议用同一类图片或同一个数据集进行训练, 可以先将学习率设置为 1e-3 训练 50 轮, 再改为 2e-4 训练 200 轮, 再改为 2e-5, 2e-6 分别训练 500, 1000 轮. 每次训练好先看一下效果再决定是否继续训练. 如果训练轮次太高可能会出现 loss 上升, 效果反而变差, 所以继续训练时先备份一下上一个模型.
训练图尺寸和 batch_size 根据你的显存调整, 一般 6G 以内建议用 32×32, 12~24G 用 64×64, 不建议 128×128 或更高, 显存会达到恐怖的 78G , 需要专业计算卡, 除非改用很小的 batch_size
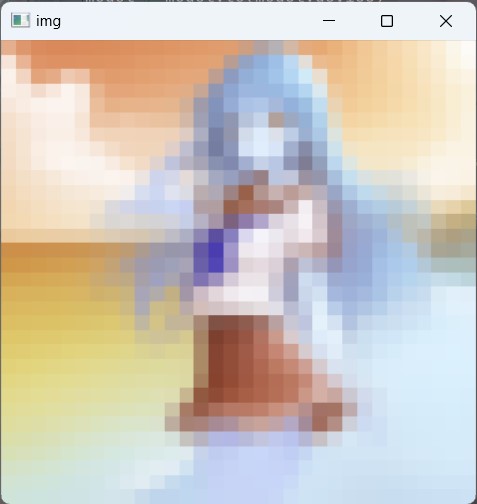
下面是我提供的训练集和模型, 对应的尺寸为 32×32, 在 generate.py 里面修改.未来可能会上传其他尺寸的模型, 注意看一下文件名改一下生成尺寸.
效果如下
Data.py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import globimport os.path as pathimport numpy as npimport torchfrom PIL import Imagefrom torchvision import transformsdef save_to_file (size: int = 64 , img_dir: str = './images/' , file: str = './images/img.pth' ): data_transforms = [ transforms.Resize((size, size)), transforms.ToTensor(), transforms.Lambda(lambda t: (t * 2 ) - 1 ) ] data_transform = transforms.Compose(data_transforms) files = sorted (glob.glob(path.join(img_dir, '*' ))) images = [data_transform(Image.open (file)) for file in files] images = torch.tensor(np.array(images), dtype=torch.float32) torch.save(images, file) if __name__ == '__main__' : save_to_file(size=64 , img_dir='./images/256/' , file='./images/girls_64.pth' )
DDPModel.py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 import mathimport numpy as npimport torchimport torch.nn as nnimport torch.nn.functional as Ffrom tqdm import tqdmdef timestep_embedding (timesteps, dim, max_period=10000 ): """ timestep 正弦嵌入 :param timesteps: a 1-D Tensor of N indices, one per batch element. These may be fractional. :param dim: the dimension of the output. :param max_period: controls the minimum frequency of the embeddings. :return: an [N x dim] Tensor of positional embeddings. """ half = dim // 2 freqs = torch.exp( -math.log(max_period) * torch.arange(start=0 , end=half, dtype=torch.float32) / half ).to(device=timesteps.device) args = timesteps[:, None ].float () * freqs[None ] embedding = torch.cat([torch.cos(args), torch.sin(args)], dim=-1 ) if dim % 2 : embedding = torch.cat([embedding, torch.zeros_like(embedding[:, :1 ])], dim=-1 ) return embedding class ResNet (nn.Module): def __init__ (self, channel_input: int , channel_output: int , channel_time: int , device: str = 'cpu' ): """ :param channel_input: 输入通道数 :param channel_output: 输出通道数 :param channel_time: 时间通道数 """ super ().__init__() self.conv1 = nn.Sequential( nn.GroupNorm(32 , channel_input, device=device), nn.SiLU(), nn.Conv2d(channel_input, channel_output, kernel_size=3 , padding=1 ) ) self.time_embedding = nn.Sequential( nn.SiLU(), nn.Linear(channel_time, channel_output) ) self.conv2 = nn.Sequential( nn.GroupNorm(32 , channel_output, device=device), nn.SiLU(), nn.Conv2d(channel_output, channel_output, kernel_size=3 , padding=1 ) ) if channel_input == channel_output: self.shortcut = nn.Identity() else : self.shortcut = nn.Conv2d(channel_input, channel_output, kernel_size=1 ) self.to(device) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: """ :param x: [batch_size, channel_input, h, w] :param t: [batch_size, channel_time] :return: [batch_size, channel_output, h, w] """ result = self.conv1(x) result += self.time_embedding(t)[:, :, None , None ] result = self.conv2(result) return result + self.shortcut(x) class AttentionBlock (nn.Module): def __init__ (self, in_channels, device='cpu' ): super ().__init__() self.query_conv = nn.Conv2d(in_channels, in_channels // 8 , kernel_size=1 , bias=False ) self.key_conv = nn.Conv2d(in_channels, in_channels // 8 , kernel_size=1 , bias=False ) self.value_conv = nn.Conv2d(in_channels, in_channels, kernel_size=1 , bias=False ) self.to(device) def forward (self, x, t ): batch_size, channels, height, width = x.shape query = self.query_conv(x).view(batch_size, -1 , height * width).permute(0 , 2 , 1 ) key = self.key_conv(x).view(batch_size, -1 , height * width) value = self.value_conv(x).view(batch_size, -1 , height * width) attention = torch.bmm(query, key) / math.sqrt(key.shape[1 ]) attention = F.softmax(attention, dim=-1 ) out = torch.bmm(value, attention.permute(0 , 2 , 1 )) out = out.view(batch_size, channels, height, width) out = out + x return out class DownSample (nn.Module): def __init__ (self, channels: int , device: str = 'cpu' ): super ().__init__() self.op = nn.Conv2d(channels, channels, kernel_size=3 , stride=2 , padding=1 ) self.to(device) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: """ 返回下采样后的图 :param x: [channel, h, w] :param t: 占位 :return: [channel, h, w] """ return self.op(x) class UpSample (nn.Module): def __init__ (self, channels: int , device: str = 'cpu' ): super ().__init__() self.op = nn.Conv2d(channels, channels, kernel_size=3 , padding=1 ) self.to(device) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: """ 返回上采样后的图 :param x: [channel, h, w] :param t: 占位 :return: """ x = F.interpolate(x, scale_factor=2 , mode="nearest" ) x = self.op(x) return x class ModuleList (nn.Module): def __init__ (self, *args ): super ().__init__() self.module_list = [] for idx, module in enumerate (args): self.module_list.append(module) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: for module in self.module_list: x = module(x, t) return x class ModuleAdapter (nn.Module): def __init__ (self, module ): super ().__init__() self.module = module def forward (self, x: torch.Tensor, t: torch.Tensor ): return self.module(x) class UNetModel (nn.Module): def __init__ (self, channel_input: int = 3 , channel_output: int = 3 , channel_model: int = 128 , channel_time: int = 512 , device: str = 'cpu' ): super ().__init__() self.channel_input = channel_input self.channel_output = channel_output self.channel_model = channel_model self.time_embedding = nn.Sequential( nn.Linear(channel_model, channel_time), nn.SiLU(), nn.Linear(channel_time, channel_time) ) self.down_blocks = nn.ModuleList([ ModuleAdapter(nn.Conv2d(3 , 128 , kernel_size=3 , stride=1 , padding=1 )), ResNet(128 , 128 , channel_time, device=device), ResNet(128 , 128 , channel_time, device=device), DownSample(128 , device=device), ModuleList( ResNet(128 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ), ModuleList( ResNet(256 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ), DownSample(256 , device=device), ResNet(256 , 256 , channel_time, device=device), ResNet(256 , 256 , channel_time, device=device), DownSample(256 , device=device), ResNet(256 , 256 , channel_time, device=device), ResNet(256 , 256 , channel_time, device=device), ]) self.up_blocks = nn.ModuleList([ ResNet(512 , 256 , channel_time, device=device), ResNet(512 , 256 , channel_time, device=device), ModuleList( ResNet(512 , 256 , channel_time, device=device), UpSample(256 , device=device), ), ResNet(512 , 256 , channel_time, device=device), ResNet(512 , 256 , channel_time, device=device), ModuleList( ResNet(512 , 256 , channel_time, device=device), UpSample(256 , device=device), ), ModuleList( ResNet(512 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ), ModuleList( ResNet(512 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ), ModuleList( ResNet(384 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), UpSample(256 , device=device), ), ResNet(384 , 128 , channel_time, device=device), ResNet(256 , 128 , channel_time, device=device), ResNet(256 , 128 , channel_time, device=device), ]) self.middle = ModuleList( ResNet(256 , 256 , channel_time, device=device), AttentionBlock(256 , device=device), ResNet(256 , 256 , channel_time, device=device), ) self.out = nn.Sequential( nn.GroupNorm(32 , 128 , device=device), nn.SiLU(), nn.Conv2d(128 , 3 , kernel_size=3 , padding=1 ) ) self.to(device) def forward (self, x: torch.Tensor, t: torch.Tensor ) -> torch.Tensor: """ :param x: :param t: :return: """ emb = self.time_embedding(timestep_embedding(t, self.channel_model)) hs = [] h = x for module in self.down_blocks: h = module(h, emb) hs.append(h) h = self.middle(h, emb) for module in self.up_blocks: temp = torch.cat([h, hs.pop()], dim=1 ) h = module(temp, emb) return self.out(h) class DDPM (nn.Module): def __init__ (self, timestep: int = 1000 , beta_start: int = 0.0001 , beta_end: int = 0.02 , device: str = 'cpu' ): """ :param timestep: 步数, 默认为 1000 :param beta_start: beta起始值 :param beta_end: beta结束值 :param tensor_range: 数据集转为tensor的范围: [-range, range] """ super ().__init__() self.timestep = timestep self.beta_start = beta_start self.beta_end = beta_end self.device = device self.unet = UNetModel(device=self.device) self.beta_list = torch.linspace(beta_start, beta_end, timestep, dtype=torch.float32, device=self.device) self.alpha_list = 1 - self.beta_list self.alpha_bar_list = torch.cumprod(self.alpha_list, dim=0 ) self.alpha_bar_prev_list = F.pad(self.alpha_bar_list[:-1 ], (1 , 0 ), value=1. ) self.sqrt_alpha_list = torch.sqrt(self.alpha_list) self.sqrt_alpha_bar_list = torch.sqrt(self.alpha_bar_list) self.sqrt_one_minus_alpha_bar_list = torch.sqrt(1 - self.alpha_bar_list) self.one_divide_sqrt_alpha_list = 1. / self.sqrt_alpha_list self.beta_divide_sqrt_one_minus_alpha_bar_list = self.beta_list / (1. - self.alpha_bar_list).sqrt() self.sigma_tilde_2 = self.beta_list * (1. - self.alpha_bar_prev_list) / (1 - self.alpha_bar_list) def get_loss (self, x: torch.Tensor ) -> torch.Tensor: """ :param x: [batch_size, 3, w, h] :return: 损失 """ batch_size = x.shape[0 ] noise = torch.randn_like(x, dtype=torch.float32, device=self.device) timestep_list = torch.randint(0 , self.timestep, (batch_size,), device=self.device) sqrt_alpha_bar = self.sqrt_alpha_bar_list.take(timestep_list).view(batch_size, 1 , 1 , 1 ) sqrt_one_minus_alpha_bar = self.sqrt_one_minus_alpha_bar_list.take(timestep_list).view(batch_size, 1 , 1 , 1 ) x_t = (sqrt_alpha_bar * x + sqrt_one_minus_alpha_bar * noise) noise_predict = self.unet(x_t, timestep_list) loss = F.mse_loss(noise, noise_predict) return loss @torch.no_grad() def generate (self, size: tuple = (64 , 64 noise: torch.Tensor = None , video: bool = False ) -> np.ndarray: """ 生成图像 :param size: 尺寸 :param noise: 随机噪声 :param video: 是否导出视频, False则导出图片 :return: 导出图片: [width, height, channel] 导出视频: [time, width, height, channel], 其中 time 取值范围为 [0, timestep - 1] """ width = size[0 ] height = size[1 ] if noise is None : x = torch.randn(size=(1 , 3 , width, height), dtype=torch.float32, device=self.device) else : x = noise.to(self.device) if video: imgs = torch.empty(self.timestep, 1 , 3 , width, height, device=self.device) imgs[0 , :, :, :, :] = x for t in tqdm(range (self.timestep - 1 , 0 , -1 )): t = torch.ones(size=(1 ,), dtype=torch.long, device=self.device) * t epsilon_t = self.unet(x, t) epsilon = torch.randn(size=(1 , 3 , width, height), dtype=torch.float32, device=self.device) x = self.one_divide_sqrt_alpha_list.take(t).view(1 , 1 , 1 , 1 ) * ( x - self.beta_divide_sqrt_one_minus_alpha_bar_list.take(t).view(1 , 1 , 1 , 1 ) * epsilon_t) x = x + self.sigma_tilde_2.take(t).view(1 , 1 , 1 , 1 ) * epsilon if video: imgs[self.timestep - t, :, :, :, :] = x if video: imgs = ((imgs.squeeze(dim=1 ).permute(0 , 2 , 3 , 1 ) + 1 ) * 255 / 2 ).round ().clamp(0 , 255 ).int () imgs = imgs.cpu().numpy() imgs = np.array(imgs, np.uint8) return imgs else : x = ((x.squeeze(dim=0 ) + 1 ) * 255 / 2 ).round ().clamp(0 , 255 ).int () x = x.permute(1 , 2 , 0 ).cpu().numpy() x = np.array(x, np.uint8) return x
train.py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 import argparseimport datetimeimport osimport sysimport torchimport yamlfrom tqdm import tqdmfrom DDPModel import DDPMdef log (info: str ) -> None : info = datetime.datetime.now().strftime('[%Y-%m-%d %H:%M:%S] ' ) + info print (info) log('start running...' ) parser = argparse.ArgumentParser() parser.add_argument('-d' , '--device' , type =str , default=None , help ='The device used for training, like: "cuda0,1,2" or "cpu"' ) parser.add_argument('-c' , '--config' , type =str , default='default' , help ='Configuration item' ) parser.add_argument('-g' , '--nogui' , help ='Hide the progress bar' , action='store_true' ) args = parser.parse_args() if args.device is None : device = 'cuda' if torch.cuda.is_available() else 'cpu' elif args.device.startswith('cuda' ): os.environ['CUDA_VISIBLE_DEVICES' ] = args.device[4 :] device = 'cuda:' + ',' .join([str (i) for i in range (len (args.device[4 :].split(',' )))]) elif args.device == 'cpu' : device = 'cpu' else : raise 'Wrong Device: ' + args.device if device.startswith('cuda' ): log('use gpu: ' + ',' .join(torch.cuda.get_device_name(i) for i in range (torch.cuda.device_count()))) else : log('use cpu' ) with open ('./config.yml' , 'r' , encoding='utf-8' ) as f: yml = yaml.load(f.read(), Loader=yaml.FullLoader) yml = yml[args.config] batch_size = yml['batch_size' ] timestep = yml['timestep' ] epochs = yml['epochs' ] lr = eval (yml['lr' ]) continue_train = yml['continue' ] autosave_epoch = yml['autosave_epoch' ] model_pth = yml['model_pth' ] check_point_pth = yml['check_point_pth' ] img_pth = yml['image_pth' ] log('loading dataset from: ' + img_pth) dataset = torch.load(img_pth) dataset = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True , drop_last=True ) model = DDPM(timestep=timestep, device=device) if os.path.isfile(check_point_pth): log('loading checkpoint...' ) check_point = torch.load(check_point_pth) model.unet = check_point['unet' ].to(device) start = check_point['epoch' ] + 1 log('epoch will start from: ' + str (start)) elif continue_train: if os.path.isfile(model_pth): log('continue training: ' + model_pth) model.unet = torch.load(model_pth) else : log('failed to continue training' ) start = 1 else : log('new training' ) start = 1 model.unet.train() optimizer = torch.optim.Adam(model.parameters(), lr=lr) log('start training...' ) if not args.nogui: gui = tqdm(total=(epochs - start + 1 ) * len (dataset), file=sys.stdout) gui.set_description('' ) for epoch in range (start, epochs + 1 ): last_autosave = 0 for idx, images in enumerate (dataset): optimizer.zero_grad() images = images.to(device) loss = model.get_loss(images) loss.backward() optimizer.step() if not args.nogui: gui.set_postfix(loss='{:.6f}' .format (loss), epoch=epoch, last_autosave=last_autosave) gui.update(1 ) if autosave_epoch != 0 and epoch % autosave_epoch == 0 and epoch != epochs: last_autosave = epoch check_point = { 'epoch' : epoch, 'unet' : model.unet } torch.save(check_point, check_point_pth) if args.nogui: log('autosave with epoch={}, loss={:.6f}' .format (epoch, loss)) if not args.nogui: gui.close() if os.path.isfile(check_point_pth): os.remove(check_point_pth) log('train finish' ) torch.save(model.unet, model_pth) log('save to: ' + model_pth)
generate.py 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 import cv2from DDPModel import *video_path = 'result/example.mp4' model = DDPM(device='cuda' ) model.unet = torch.load('./model/model.pth' ) model.unet.eval () model = model.to(model.device) size = 64 if isinstance (size, int ): size = (size, size) img = model.generate(size=size, video=False ) if len (img.shape) == 3 : cv2.namedWindow('img' , 0 ) cv2.resizeWindow('img' , 512 , 512 ) cv2.imshow('img' , img) cv2.waitKey(0 ) else : video = cv2.VideoWriter( video_path, cv2.VideoWriter.fourcc(*'mp4v' ), 60 , size, True ) for x in img: video.write(x) video.release()
config.yml 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 default: batch_size: 128 timestep: 1000 epochs: 500 lr: 2e-4 continue: true autosave_epoch: 20 model_pth: './model/model.pth' check_point_pth: './model/checkpoint.pth' image_pth: './images/girls.pth' server: batch_size: 128 timestep: 1000 epochs: 500 lr: 2e-4 continue: true autosave_epoch: 20 model_pth: './model/model.pth' check_point_pth: './model/checkpoint.pth' image_pth: './images/girls.pth'
我还试了一下用一张图片复制N次进行训练, 效果特别好(如果仅仅是展示可以糊弄一下, 做研究的这么搞后果自负)
生成过程
Your browser does not support the video tag.