算法基础-二叉搜索树

二叉搜索树的概念

二叉搜索树是一种特殊的二叉树,对于其中的任意结点 x,其左子树中的任何结点的值都小于结点 x 的值,其右子树中的任何结点的值都大于结点 x 的值

二叉搜索树的结点

struct Node{
    int value;
    Node* lChild;
    Node* rChild;
};

因此只需要对二叉搜索树进行中序遍历,就可以升序输出所有元素

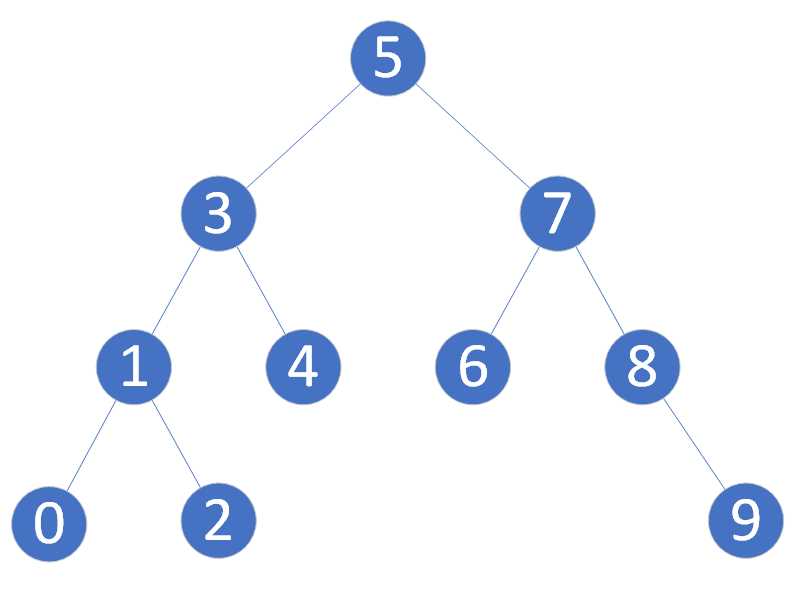
查询

为了查找二叉搜索树中是否存在value为key的项,我们可以采用递归的方法,如果当前结点不是要查找的项,则比较value和key的大小,以确定接下来需要访问左子树还是右子树

Node* Search(Node* node, int key){
    if(node == NULL || node->value == key) {
        return node;
    }else{
        return key > node->value
        ? Search(node->rChild, key)
        : Search(node->lChild, key);
    }
}

插入

二叉搜索树的插入操作与查询类似,都是不断地向下查找,直到找到一个子树为NULL的结点

例如上面的图片,如果往其中插入一个值: 20,那么这个值会被添加到 “9” 结点的右子树上

bool Insert(Node *node, int key) {
    assert(node != NULL);
    if (key < node->value) {
        if (node->lChild != NULL) {
            return Insert(node->lChild, key);
        } else {
            node->lChild = (Node *) malloc(sizeof(Node));
            node = node->lChild;
            node->lChild = node->rChild = NULL;
            node->value = key;
            return true;
        }
    } else if (key > node->value) {
        if (node->rChild != NULL) {
            return Insert(node->rChild, key);
        } else {
            node->rChild = (Node *) malloc(sizeof(Node));
            node = node->rChild;
            node->rChild = node->rChild = NULL;
            node->value = key;
            return true;
        }
    } else {
        return false;
    }
}

删除

删除操作较为复杂,删除一个结点时会出现3种情况

被删除的结点 x 没有子结点,那么只需要用NULL来替换父结点的子结点
被删除的结点 x 有一个子结点,那么只需要把父结点的子结点修改为 x 的子结点
被删除的结点 x 有两个子结点,此时情况较为复杂,我们需要从右子树中选取一个结点来替换 x 结点.考虑到二叉搜索树有一个特性: 右子树中的所有值一定比自己结点的值都要大.因此我们只需要选出右子树中最小值 y 来替换 x 结点,这样右子树中的剩余部分一定都比 y 更大.同理,也可以选出左子树中的最大值 n 来替换 x 结点.在删除最小值(最大值)结点时,可以递归调用自己,因为最值结点不可能存在两个子结点