非线性结构的概念
线性结构是指逻辑上各个结点一一对应的关系,例如链表,即使它在储存上可能并不是顺序储存
非线性结构是指逻辑上存在一对多关系的结点的结构,例如树,图等.它们的任何结点都可能对应着其它多个不同的结点
有根树
二叉树
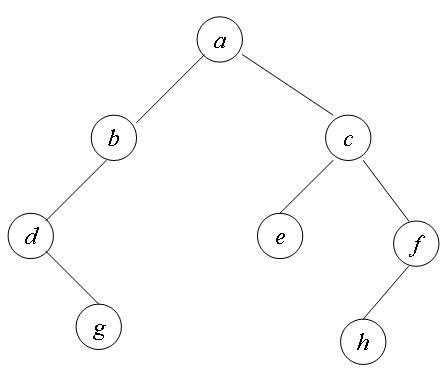
二叉树在逻辑上是一种树状结构,最顶上的结点被称为根结点,每个结点都有 key, lChild和rChild值,分别记录该结点的值,左子树指针和右子树指针,当key为空(NULL)时,该结点为根结点.二叉树的左右子树可能为空,也可能根本就没有左右子树,但是除了左右子树以外,不能出现第三棵子树
多叉树
若将二叉树的左右子树推广到无限制子树的结构,便成为多叉树.多叉树的子树数量是不确定的,因此需要用链表储存
下面给出实现多叉树结构的代码
1
2
3
4
5
6
7
8
9
10
11
12
| struct Node;
struct Tree;
struct Node{
Tree* tree;
Node* next;
};
struct Tree{
int value;
Node* child;
};
|
树的遍历
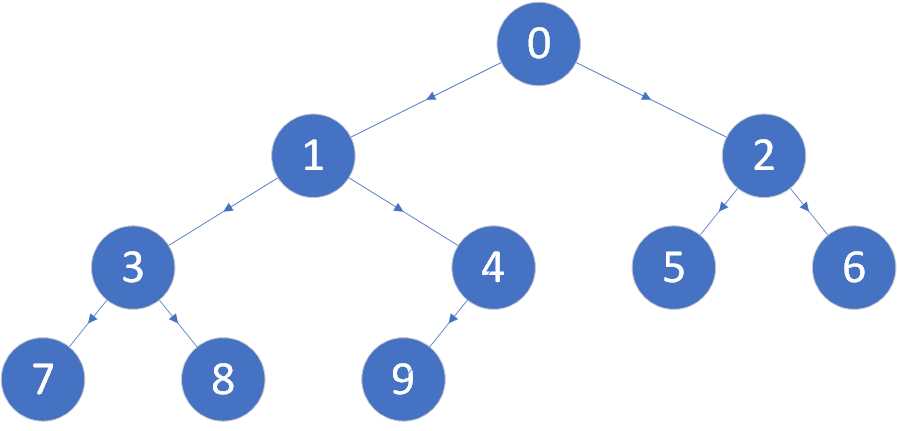
现有一棵如下图所示的二叉树
深度优先遍历
深度优先遍历的思想是先访问完当前结点对应的整个子树,然后再访问另一个结点
1
2
3
4
5
6
7
| void DFS(Tree* tree){
if(tree != NULL){
DFS(tree->lChild);
printf("%d ",tree->value);
DFS(tree->rChild);
}
}
|
在上面的代码中,先访问了当前结点的左子树,然后才输出自己结点,最后访问右子树,该遍历方法属于中序遍历,即输出自己结点的代码位于输出左右子树结点的代码的中间,输出顺序为:左子树→自己→右子树
同理先序遍历的顺序为:自己→左子树→右子树
先序遍历的顺序为:左子树→右子树→自己
上图所示的二叉树的中序遍历顺序为:7 3 8 1 9 4 0 5 2 6
广度优先遍历
广度优先遍历需要借助队列实现,它按照结点的深度顺序输出结点.首先把根结点加入队列,从根节点开始,每当输出一个结点,就把它的子节点全部加入队列,直到队列为空
1
2
3
4
5
6
7
8
9
10
11
12
13
| void BFS(Tree* tree){
if(tree == NULL) return;
queue<Tree*>* q = new queue<Tree*>();
q->push(tree);
while (!q->empty()){
Tree* front = q->front();
q->pop();
printf("%d ",front->value);
if(front->lChild != NULL) q->push(front->lChild);
if(front->rChild != NULL) q->push(front->rChild);
free(front);
}
}
|
上图所示二叉树的广度优先遍历顺序为:0 1 2 3 4 5 6 7 8 9
图
对于图的概念,可以参考下列文章
人工智能基础-图论初步 - DearXuan的主页
矩阵法
使用矩阵 M 来表示图 G,将 G 中的每个结点量化为一个数字,M(i,j)=0表示 G 中 i 和 j 所代表的结点不相邻,M(i,j)=1表示 G 中 i 和 j 代表的结点相邻
显然同一个图 G 中结点 V 的个数是固定的,设为 n,因此矩阵 M 是一个 n 阶的方阵
例如以下无向图
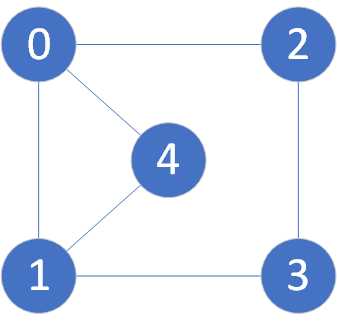
它用矩阵表示为
| 0 | 1 | 2 | 3 | 4 |
|---|
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 1 | 1 | 0 |
| 3 | 0 | 1 | 1 | 1 | 0 |
| 4 | 1 | 1 | 0 | 0 | 1 |
实际上 M(i,j) 除了表示相邻状态以外,还可以用来表示权值,例如路径长度,只需要把 1 改成具体权重即可,这时 0 可能会引起误解,因此我们可以定义一个特殊的或者正常情况下不可能取到的数来表示不相邻,例如 -1 或 999
邻接链表法
当边数远小于顶点数时,采用矩阵表示会严重浪费空间
邻接链表法将图 G 的所有顶点具体化为一个结点,并保存在长度固定的数组中,每个结点都储存了当前结点的值和图 G 中对应顶点的所有边
1
2
3
4
5
6
7
8
9
| struct Vertex{
int value;
Edge* edge;
};
struct Edge{
Vertex* vertex;
Edge* next;
};
|
图的遍历
与二叉树类似,图的遍历也可以分为深度优先遍历和广度优先遍历,但不同之处在于,二叉树中不存在回路,而图中存在回路,所以会出现重复遍历的情况,因此我们需要给每个结点额外增加一个变量,以储存该结点是否已经被访问过
1
2
3
4
5
6
7
8
9
10
| struct Vertex{
int value;
bool isVisited;
Edge* edge;
};
struct Edge{
Vertex* vertex;
Edge* next;
};
|
深度优先遍历
每当访问一个结点时,如果该结点存在多个相邻结点,则按顺序把其中一个相邻结点的全部相邻结点都访问完,再访问另一个相邻结点
1
2
3
4
5
6
7
8
9
10
11
12
13
| void DFS(Vertex* vertex){
if(vertex != NULL){
printf("%d ",vertex->value);
vertex->isVisited = true;
}
Edge* edge = vertex->edge;
while (edge != NULL){
if(!edge->vertex->isVisited){
DFS(edge->vertex);
}
edge = edge->next;
}
}
|
一个结点开始进行深度优先搜索的时间点称为发现时间,搜索完该结点所有边的时间点称为结束时间
广度优先遍历
每当访问一个结点时,先把该结点的相邻结点全部访问完,再访问相邻结点的相邻结点,即一层层访问下去
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| void BFS(Vertex* vertex){
queue<Vertex*> q;
q.push(vertex);
while (!q.empty()){
Vertex* front = q.front();
printf("%d ",front->value);
front->isVisited = true;
q.pop();
Edge* edge = front->edge;
while (edge != NULL){
if(!edge->vertex->isVisited){
q.push(edge->vertex);
edge->vertex->isVisited = true;
}
edge = edge->next;
}
}
}
|
拓扑序列
偏序关系
将有向图 G 中的所有顶点看作一个集合,图 G 中的每个有向边都是关于集合中两个顶点的关系,若有向图 G 中不存在回路,则有向图 G 中的每条边共同构成了一个偏序关系.如果存在从顶点 A 到顶点 B 的通路,则称 A 在 B 的前面
线性次序
将有向图 G 中的所有顶点线性排列,使得任意标注一条有向边后,都是从左指向右边
拓扑排序
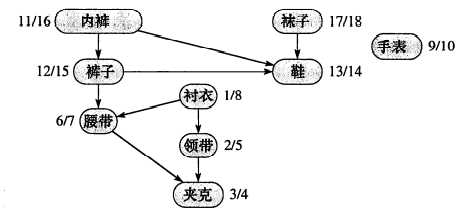
上面的经典例题展示了每天起床穿衣服的先后次序,边上的数字为深度优先搜索的发现时间和结束时间
将其用数字表示
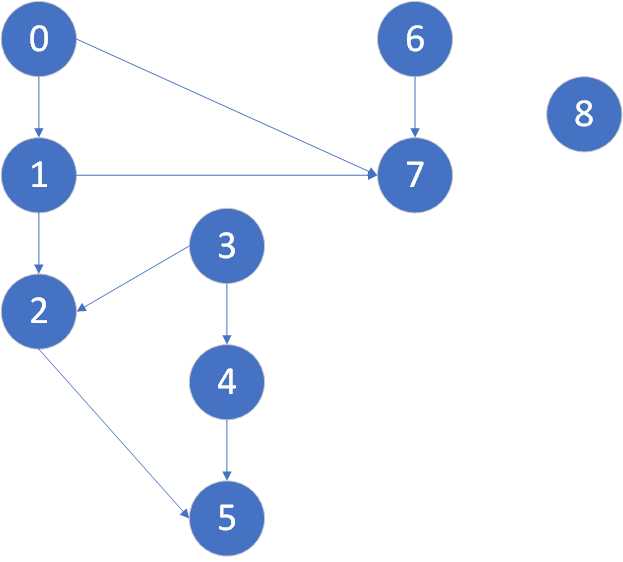
我们可以从图中得到一个拓扑序列:
这样无论我们标出哪一条有向边,它在拓扑序列上总是从左边指向右边
实际上这个序列恰好是深度优先搜索的结束时间的降序,下面我们用代码来求出这个图的各个顶点的发现时间和结束时间,我们将发现时间和结束时间作为顶点的参数添加到结构体内
1
2
3
4
5
6
7
8
9
10
11
12
| struct Vertex{
int index;
int startTime;
int endTime;
bool isVisited;
Edge* edge;
};
struct Edge{
Vertex* vertex;
Edge* next;
};
|
将原本的图用一个类来表示
1
2
3
4
5
6
7
8
9
10
11
12
| class Graph{
public:
int size;
Graph(int size);
void addEdge(int edge1, int edge2);
Vertex* get(int index);
void GetDFSTime();
private:
Vertex** G;
void DFS(int index, int* order);
};
|
下面是具体实现代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| Graph::Graph(int size) {
this->size = size;
G = (Vertex**) malloc(size * sizeof(Vertex));
for(int i=0;i<size;i++){
G[i] = (Vertex*)malloc(sizeof(Vertex));
G[i]->index = i;
G[i]->isVisited = false;
G[i]->edge = NULL;
}
}
void Graph::addEdge(int edge1, int edge2) {
Edge* edge = (Edge*)malloc(sizeof(Edge));
edge->vertex = G[edge2];
edge->next = NULL;
if(G[edge1]->edge == NULL){
G[edge1]->edge = edge;
}else{
Edge* e = G[edge1]->edge;
while (e->next != NULL){e = e->next;}
e->next = edge;
}
}
Vertex* Graph::get(int index) {
if(index < 0 || index >= size){
return NULL;
}else{
return G[index];
}
}
void Graph::GetDFSTime(){
int order = 0;
for(int i=0;i<size;i++){
DFS(i,&order);
}
for(int i=0;i<size;i++){
printf("index =%2d: %2d, %2d\n",G[i]->index, G[i]->startTime, G[i]->endTime);
}
}
void Graph::DFS(int index, int* order){
Vertex* vertex = get(index);
if(vertex == NULL || vertex->isVisited) return;
G[index]->startTime = ++(*order);
vertex->isVisited = true;
Edge* edge = vertex->edge;
while (edge != NULL){
if(!edge->vertex->isVisited){
DFS(edge->vertex->index, order);
}
edge = edge->next;
}
G[index]->endTime = ++(*order);
}
|
进行测试
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| int main()
{
Graph g(9);
g.addEdge(0,1);
g.addEdge(0,7);
g.addEdge(1,2);
g.addEdge(1,7);
g.addEdge(2,5);
g.addEdge(3,2);
g.addEdge(3,4);
g.addEdge(4,5);
g.addEdge(6,7);
g.GetDFSTime();
}
|
得到运行结果
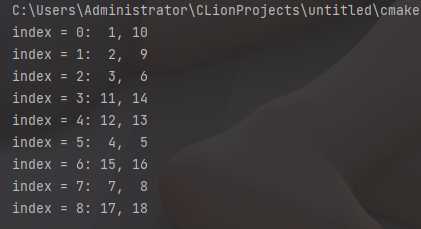
将各个顶点按结束时间(第二个)降序排列,得到的序列即是拓扑序列
DFS与拓扑序列的关系
在上面的代码中,我们直接用DFS的结束时间来作为拓扑排序的依据,下面给出依据
我们只需要证明:如果存在从 A 到 B 的有向边,则 A 的结束时间大于 B 的结束时间
我们知道,在深度优先遍历中,如果存在从 A 到 B 的有向边,那么DFS会先访问 A,然后访问 B,等访问完 B 的全部子结点后,才会回溯到 A,因此 B 总是在 A 之前结束,即 A 的结束时间大于 B 的结束时间














