算法基础-函数渐近

渐近等价

考虑函数: $f(x)=x^2+4x$

当 $x\rightarrow \infty$ 时,该函数可以看作 $x^2$ 与它的高阶无穷小 $o(x^2)$ 之和,即

f(x)=x^2+4x=x^2+o(x^2)

于是我们称 $f(x)$ 和 $x^2$ 是渐近等价的,设 $g(x)=x^2$ ,那么我们可以用下面的符号表示渐进等价

f(x) \sim g(x)

更一般地,如果存在两个函数 $f(x)$ 和 $g(x)$ ,使得下面式子成立

f(x)=g(x)+o(g(x))

就称 $f(x)$ 和 $g(x)$ 渐进等价

你也可以用极限的方法来判断两个函数是否渐近等价

\lim\limits_{x\rightarrow \infty}\frac{f(x)}{g(x)}=1

我们可以轻而易举地得到一个结论： $f(x)$ 总是跟自己渐近等价

f(x) \sim f(x)

若对于函数 $f(n)$ , $g(n)$ ,存在 $c$ 和 $k$ ,使得

c>k \rightarrow 0\leq f(n) \leq cg(n)

即从 $k$ 开始, $f(n)$ 永远无法超过 $cg(n)$ ,则称 $g(n)$ 为 $f(n)$ 的渐近上界,写作

f(n)=O(g(n))

注意 $O(g(n))$ 表示的是一个集合,它代表了所有以 $g(n)$ 为渐近上界的函数,此处的等于号是用于指出 $f(n)$ 是所有以 $g(n)$ 为渐近上界的函数里的一员

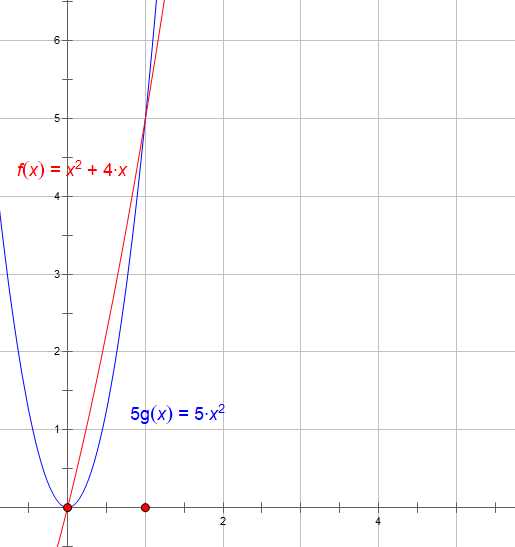
下面的图片可以帮助你更好的理解 $f(n)$ 与 $g(n)$ 的关系

若选取 $c=5$ ,则当 $x>1$ 时, $f(n)<5g(n)$

同样的,我们也可以轻易得到一个结论, $f(x)$ 总是自己的渐近上界

f(x)=O(f(x))

设有下面一段函数

for(int i=1;i<=n;i++){
    for(int j=1;j<=i;j++){
        swap(i,j);
    }
}

外循环共执行了n次,内循环共执行了i次,所以总共执行次数为

S(n)=\sum\limits_{i=1}^{n}i=\frac{n^2+n}{2}

如果我们把代码改成如下所示

for(int i=1;i<=n;i++){
    for(int j=1;j<=i;j++){
        execute1(i,j);
        execute2(i,j);
        execute3(i,j);
        execute4(i,j);
    }
}

那么此时算法执行命令的总次数就翻了4倍,随着n的逐渐增大,这两个算法所用时间的增长规模是相似的,并且我们并不需要特别高的精度.因此我们可以用算法执行时间 $t(n)$ 的渐近上界 $f(n)$ 来表示一个算法的效率

f(n)=O(f(n))=O\left(\frac12n^2+\frac12n\right)

在渐近时间复杂度中,我们只关心执行时间的增长规模,而不关心具体数字,显然以下两个函数的规模是一致的

\left\{ \begin{array}{ll} f(n)=\frac12n^2+\frac12n \\\\ g(n)=\frac12n^2+\frac32n \end{array} \right.

因此我们需要对渐近时间复杂度进行化简

根据定义,我们得到

\left\{ \begin{array}{ll} 0 \leq f(n) \leq c_1g(n),n\geq n_1 \\\\ 0 \leq g(n) \leq c_2h(n),n\geq n_2 \end{array} \right.

合并,得到

0 \leq f(n) \leq c_1c_2h(n),n>\max \{n_1,n_2\}

命题得证

我们设 $h(x) = O(f(x))$ ,由渐近等价得定义得

f(x)=g(x)+o(g(x))

由无穷小定义可得,对于任意 $ε>0$ ,总存在 $N$ ,使得下列不等式成立

o(g(x))<εg(x),x>N

取 $ε=1$ ,便得到

g(x)+o(g(x))<2g(x),x>N

替换掉 $f(x)$ ,得到

0 \leq h(x) \leq cf(x) \leq 2cg(x)

命题得证

通过上面两个结论,再利用其它高等数学知识,我们便可以推出下面的结论

\begin{array}{ll} 1. &f(x)+g(x)=O(f(x)+g(x)) \\\\ 2. &O(k)=O(1) \\\\ 3. &O(kx)=O(x) \\\\ 4. &O(x^n+o(x^n))=O(x^n) \end{array}

因此,在计算渐近时间复杂度时,若出现多项式,我们可以遵守以下准则

例如: $O(4n^3+2n^2+9)=O(n^3)$