算法基础-算法分析

算法

什么是算法

算法是对特定问题求解步骤的一种描述,是执行的有限序列,其中每个指令都表示一个或多个操作.

如果想要从一个数组中查找指定的数字key并返回位置,只需要从第一个位置开始遍历整个数组,直到找到给定的key并返回位置.这就是一种算法.

为什么要用算法

算法无处不在.

为了走出迷宫,你可能需要DFS,即深度优先搜索算法来寻找出路.
为了找到最短路径,你可能要用到A*算法来高效查找.
为了将一串数字排序,你需要用更快的快速排序算法,而不是一个一个比较.

显然,上面的三个问题都有许多种不同的解法,但是不同解法的效率和准确度大相径庭.为了寻找一个正确的解法或者找到更优的解法,就需要用到算法.

数据结构

数据结构是一种储存数据的方式,用来提供高效的访问和修改.任何数据结构都只对某几个用途有效,对于不同的算法,应该考虑不同的数据结构.

堆栈

堆栈是一个先进后出的数据结构,类似于汉诺塔,每次只能在最顶上插入数据,想要去除下面的数据就必须先把上面的数据取完.

队列

队列与堆栈相反,先进去的数据最先出去,就像排队一样,也因此得名.

链表

与数组不同,链表的每个节点都储存了自己的值和下一个节点的地址,这样就可以快速地插入新节点而不需要重新排列.但是这种方法也有弊端,如果想要找到第10个数字,就需要把前9个全部找一遍.

并行与串行

根据代码执行方式不同,可将其分为并行与串行.串行是指代码严格按照先后顺序执行,并行是指代码的执行顺序可以被打乱,以至于可以在同一时间间隔内同时执行多个代码.

在计算机图形学中,每个像素点都相对独立,互不干扰,因此可以利用GPU多处理器的优势来加速执行.

算法效率

渐进时间复杂度

在一个算法中,若基本操作重复的次数可以表示为对问题规模n的函数 $f(n)$ ,那么算法的时间度量就可以记作 $T(n)=O(f(n))$

它表示随着问题规模n的增加,算法执行时间的增长率和f(n)的增长率相同.

例如下面的代码

for(int i=0;i<n;i++){
    for(int j=0;j<n;j++){
        swap(a[i],a[j]);
    }
}

显然swap操作被重复执行了 $n^2$ 次,因此它的渐进时间复杂度是 $O(n^2)$ ,简称时间复杂度

在计算时间复杂度时,通常会只保留最高阶,例如 $O(n^3+n^2+2)$ 的写法是错误的,而正确的写法应该是 $O(n^3)$

空间复杂度

空间复杂度用来度量算法所需要的储存空间的大小.

如果所需的储存空间大小与数据数据有关,则除非特别指明,均按最坏情况分析.

分治法

如果一个算法通过一次或多次调用自身来解决问题,那么这些算法就使用了分治法的思想.

分治法将一个问题划分为多个相类似但是规模更小的子问题.直接解出父问题是困难的,但是解出子问题是容易的,而子问题又可以分出别的子问题.只需要将子问题的解合并,就能计算出父问题.

归并排序

归并排序是一种典型的分治法示例,它将数组分为两个部分,将两部分分别排序后再合并为一个数组.

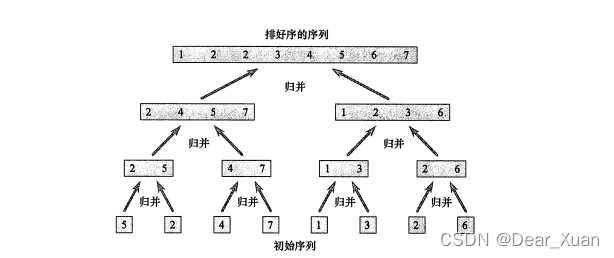
归并排序

void sort(int *list, int *result, int left, int right) {
    //如果left不小于right,则直接退出
    if (left >= right) return;
    //将数组从中间切割,mid为切割位置
    int mid = ((right - left) >> 1) + left;
    //切割后的两个数组的起始和终止位置
    int left_1 = left, right_1 = mid;
    int left_2 = mid + 1, right_2 = right;
    //将切割后的数组排序
    sort(list, result, left_1, right_1);
    sort(list, result, left_2, right_2);
    int i = left;
    //合并排序后的数组
    while (left_1 <= right_1 && left_2 <= right_2){
        result[i++] = list[left_1] < list[left_2]
                ? list[left_1++]
                : list[left_2++];
    }
    while (left_1 <= right_1){
        result[i++] = list[left_1++];
    }
    while (left_2 <= right_2){
        result[i++] = list[left_2++];
    }
    //赋值
    for (i = left; i <= right; i++){
        list[i] = result[i];
    }
}

时间复杂度

在归并排序中,我们用递归的方法来排序数组.

对于切割到最后,长度为1的数组,其时间复杂度为 $O(1)$ ,而其它情况下的时间复杂度为 $2T(\frac n2)+O(n)$

因此得到 $T(n)$ 的表达式

T(n)= \left \{ \begin{array}{ll} O(1) &,n=1 \\\\ 2T\left(\frac n2\right) &,n > 1 \end{array} \right.

简单推导便可得到下列结果

\begin{array}{ll} T(n) &=2T(\frac n2)+O(n) \\\\ &=2^2T(\frac n4)+2O(n) \\\\ &=... \\\\ &=2^kT(\frac n{2^k})+kO(n) \end{array}

由于迭代到最后, $2^k$ 次方应该等于n,所以可以直接使用 $\log n$ 来替换k,因此完整推导过程如下

\begin{array}{ll} T(n) &=2T(\frac n2)+O(n) \\\\ &=2^2T(\frac n4)+2O(n) \\\\ &=... \\\\ &=2^kT(\frac n{2^k})+kO(n) \\\\ &=nO(1)+(\log n)O(n) \\\\ &=O(n\log n) \end{array}

故归并排序的时间复杂度为 $O(n\log n)$

实际上分治法并不会只分成两个部分,还可以有 $T(\frac n3)$ 甚至 $T(\frac n4)$ ,但是归根到底都可以用迭代的方法来求出时间复杂度.