人工智能基础-局部搜索算法

爬山算法

算法概念

爬山算法类似于贪心搜索,它每次都会查找附近节点里的最优节点,并移动到最优节点,如此循环便找到最优解,但是它只能找到局部的最优解,而非整体最优解

问题示例

以搜索最高点为例,已知山坡的高度 $f(x,y)=e^{-(x^2+y^2)}+4e^{-\left((x-2)^2+(y-3)^2\right)}$ ,给定初始地点,找到最高点

显然x和y的范围是无穷大的,无法遍历全部结果,因此采用爬山算法找到局部最优解

#include <iostream>
#include <cmath>
 
using namespace std;
 
#define pai 3.141592653589
#define e 2.718281828284
#define step 0.1
#define Node _Node
 
//计算(x,y)处的高度
double f(double x, double y) {
    double x2 = x * x, y2 = y * y;
    double x_2 = (x - 2) * (x - 2), y_2 = (y - 3) * (y - 3);
    return pow(e, -(x2 + y2)) + 4 * pow(e, -(x_2 + y_2));
}
 
//节点类
class _Node {
public:
    double x;//x坐标
    double y;//y坐标
    double height;//高度
    void init(double x, double y);//初始化节点
};
 
void _Node::init(double x, double y) {
    this->x = x;
    this->y = y;
    this->height = f(x, y);
}
 
//查找附近的最高点并返回
Node Search(Node node) {
    double x = node.x;
    double y = node.y;
    Node nodes[4];
    nodes[0].init(x + step, y);
    nodes[1].init(x - step, y);
    nodes[2].init(x, y + step);
    nodes[3].init(x, y - step);
    for (Node &i: nodes) {
        //查找最高点
        if (i.height > node.height) {
            node = i;
        }
    }
    return node;
}
 
int main() {
    Node node;
    Node nearly;
    double x, y;
    scanf("%ld%lf", &x, &y);
    node.init(x, y);
    while (true) {
        nearly = Search(node);
        if (nearly.height == node.height) {
            //如果最高点是自己或者和自己一样高,说明已经找到局部最优解
            break;
        } else {
            //最高点不是自己,继续查找
            node = nearly;
        }
    }
    printf("\nx: %lf\ny: %lf\nHeight: %lf\n", node.x, node.y, node.height);
    return 0;
}

初始位置为 $(0.5, 0.5)$

初始位置为 $(5, 5)$

模拟退火算法

Metropolis准则

Metropolis准则使用随机因素来确定是否接收新状态

设时间为 $t$ , 温度为 $T$ , 状态函数 $F(t)$ ,下一状态 $F(t+1)$

接收 $(t+1)$ 状态的概率为 $P$ ,且 $P$ 满足

P= \left \{ \begin{array}{ll} 1 &,F(t+1)<F(t) \\ e^{-\frac{f(t+1)-f(t)}{kT}} &,F(t+1)\geq F(t) \end{array} \right.

其中 $k\in [0,1]$

算法概念

模拟退火算法遵循 $Metropolis$ 准则,按照一定的概率接受下一个解,即使它是非最优解,因此随着迭代次数的增加,最终会趋向于全局最优解

问题示例

已知山坡高度 $f(x)=x+\sin x-2\cos 2x$
求 $x\in[0, 20]$ 时山坡的最低点

通过图像可以看出该函数拥有多个极小值点

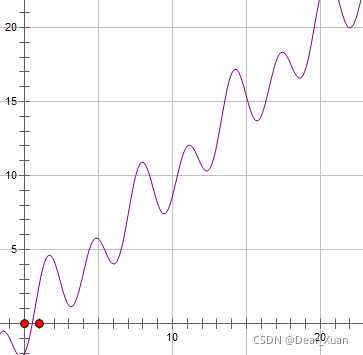
如果使用爬山算法会在其中一个极小值点结束

爬山算法

#include <iostream>
#include <cmath>
 
using namespace std;
 
#define ERROR INT32_MAX
#define step 0.1
 
double x_min = 0;//最小值
double x_max = 20;//最大值
 
//计算函数值
double f(double x) {
    if (x < x_min || x > x_max) {
        //超出界限,返回int32的最大值
        return ERROR;
    } else {
        return x + sin(x) - 2 * cos(2 * x);
    }
}
 
//使用爬山算法求解
int main() {
    double x;
    cin >> x;//输入初始位置
    double height = f(x);//状态值(高度)
    for (;;) {
        //获取x的左边和右边的状态值
        double x1 = x + step, x2 = x - step;
        double h1 = f(x1), h2 = f(x2);
        //用x1和h1保存两边的较低点
        if (h2 < h1) {
            h1 = h2;
            x1 = x2;
        }
        //将两边的较优解与当前解比较
        if (h1 < height) {
            //存在比当前位置更优的解,则向该位置移动
            x = x1;
            height = h1;
        } else {
            //两边都不存在更优的解,退出循环
            break;
        }
    }
    printf("x: %lf\nh: %lf\n", x, height);
    return 0;
}

显然 $x=12.3$ 并不是全局的最优解,而是局部最优解

现使用模拟退火算法的思路改良爬山算法:

每次从当前解周围随机取一个新的解
如果新的解更优,则直接替换当前解
如果当前解更优,则按照一定概率接受新的解

模拟退火算法

#include <iostream>
#include <cmath>
#include <sysinfoapi.h>
 
using namespace std;
 
#define step 0.1
 
double x_min = 0;//最小值
double x_max = 20;//最大值
 
double k = 0.9;
double T = 50000;//初始温度
double dT = 0.99;//下降倍率
double minT = 100;//最低温度
int num = 50000;//迭代次数
 
double x;
double height;
double x_next;
double height_next;
 
//计算函数值
double f(double x) {
    return x + sin(x) - 2 * cos(2 * x);
}
 
//获取start到end的随机数
double random(double start, double end) {
    double len = end - start;//区间长度
    double r = rand() / ((double) RAND_MAX + 1.0);//0到1之间的随机数
    return start + r * len;
}
 
//使用模拟退火算法求解
int main() {
    cin >> x;//输入初始位置
    height = f(x);
    while (T > minT) {
        //重置随机数种子
        srand(GetTickCount());
        for (int i = 0; i < num; i++) {
            //添加(-0.5, 0.5)的扰动,获取新的解
            x_next = x + random(-1, 1);
            //确保新的解不越界,否则直接跳过
            if (x_next >= x_min && x_next <= x_max) {
                height_next = f(x_next);
                if (height_next < height) {
                    //新的解更优,直接替换当前解
                    x = x_next;
                    height = height_next;
                } else {
                    //当前解更优,以一定的概率接受新的解
                    double dx = x_next - x;
                    double p = exp(dx / (T * k));
                    if (p < random(0, 1)) {
                        x = x_next;
                        height = height_next;
                    }
                }
            }
        }
        T *= dT;
    }
    printf("x: %lf\nh: %lf\n", x, height);
    return 0;
}

成功找到全局最优解