贪心算法
算法原理
贪心算法也属于启发式算法的一种.贪心算法从来不关注整体,而总是选择基于当前状态下的最优解,贪心可以看成A∗的一种特殊情况
在上一篇博客中,已经知道A∗算法的综合优先级为f(N)=g(N)+h(N),这里的只需要令g(N)=0,f(N)便是当前状态下的预计花费,只需要每次都选择h(N)最小的路径,便是当前状态下的最优解
迷宫问题
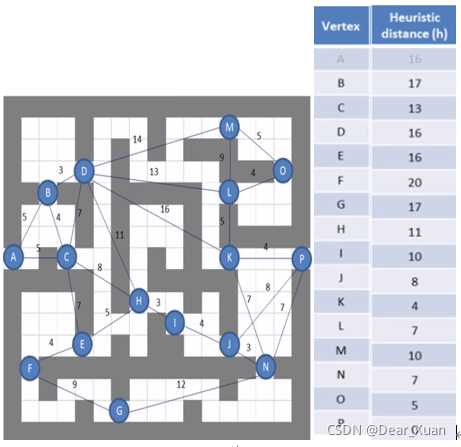
贪心算法从不关注g(N),因此只需要每次都比较相邻节点里的h(N)即可
贪心算法得到的路径为: A-C-H-I-J-P
回溯算法
算法原理
回溯算法是DFS的扩展,在DFS的基础上多了剪枝函数,剪枝函数包括约束函数和限界函数,用于判断当前节点是否符合题意,如果不符合,则原路返回.由于多了判断,因此遍历的节点比DFS更少,速度也更快
通常情况下,可以把问题的解转化成多叉树,当一个节点满足题意时,才会继续遍历它的子树,否则直接跳过当前节点
约束函数
约束函数用来排除不可能存在解的情况.例如四皇后问题中,分别在(0,0)和(2,1)位置放上皇后,此时整个棋盘只剩下(1,3)位置

显然这种情况不满足题意,因此跳过该情况对应的节点
限界函数
限界函数用来排除非最优解的情况.例如在路径规划,已经找到了一条长度为10的通路,而当前节点的g(N)已经大于10,那么当前节点的子树中不可能存在比10更短的通路,因此跳过该节点
n皇后问题
问题描述
将n个皇后放在n×n的方格纸上,使n个皇后彼此之间不在同一行,同一列,统一对角线上.给出所有摆法
状态定义
定义一维数组queen[n]来表示皇后位置,queen[i]=j表示第i行的皇后在j列,若j=-1则表示第i行没有皇后(目前没有,但是最终一定会有)
例如
1
| int queen[] = {2,0,3,1};
|
表示皇后位置如下

冲突检测
显然用一维数组表示法,不可能出现皇后在同一行的情况,因此只需要比较列和对角线
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
bool CheckConflict() {
for (int i = 0; i < N; i++) {
if(queen[i] == -1) continue;
for (int j = i + 1; j < N; j++) {
if(queen[j] == -1) continue;
if (queen[i] == queen[j]) return false;
if (abs(i - j) == abs(queen[i] - queen[j])) return false;
}
}
return true;
}
|
约束函数
约束函数CheckEnable(int i,int j)用于判断能否在(i,j)处放置皇后,如果不能,则不需要继续遍历
1
2
3
4
5
6
7
|
bool CheckEnable(int i, int j) {
queen[i] = j;
bool flag = CheckConflict();
queen[i] = -1;
return flag;
}
|
回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
void Search(int i) {
if(i >= N){
num++;
Print();
return;
}
for(int j=0;j<N;j++){
if(CheckEnable(i,j)){
queen[i] = j;
Search(i+1);
queen[i] = -1;
}
}
}
|
完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
| #include <iostream>
#include <queue>
using namespace std;
#define N 4
int queen[N];
int num = 0;
void Print();
void Search(int i);
int main() {
for (int &i: queen) {
i = -1;
}
Search(0);
printf("Total Answer: %d",num);
return 0;
}
bool CheckConflict() {
for (int i = 0; i < N; i++) {
if(queen[i] == -1) continue;
for (int j = i + 1; j < N; j++) {
if(queen[j] == -1) continue;
if (queen[i] == queen[j]) return false;
if (abs(i - j) == abs(queen[i] - queen[j])) return false;
}
}
return true;
}
bool CheckEnable(int i, int j) {
queen[i] = j;
bool flag = CheckConflict();
queen[i] = -1;
return flag;
}
void Search(int i) {
if(i >= N){
num++;
Print();
return;
}
for(int j=0;j<N;j++){
if(CheckEnable(i,j)){
queen[i] = j;
Search(i+1);
queen[i] = -1;
}
}
}
void Print(){
for(int i : queen){
for(int j=0;j<N;j++){
if(i == j){
printf("1 ");
} else{
printf("0 ");
}
}
printf("\n");
}
printf("\n");
}
|
当 n = 4 时

当 n = 8 时














