图的遍历
深度优先遍历 DFS
遍历一个节点,需要访问它自己,再遍历左子树和右子树,根据遍历顺序分为以下三种遍历
- 前序遍历:先访问当前节点,再遍历左右子树
- 中序遍历:先遍历左子树,再访问自己,最后遍历右子树
- 后序遍历:先遍历左右子树,最后访问自己
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| #include <iostream>
struct _Node{
int num;
_Node *lChild;
_Node *rChild;
};
void 前序遍历(_Node *node){
if(node == nullptr) return;
printf("num = %d\n",node->num);
前序遍历(node->lChild);
前序遍历(node->rChild);
}
void 中序遍历(_Node *node){
if(node == nullptr) return;
中序遍历(node->lChild);
printf("num = %d\n",node->num);
中序遍历(node->rChild);
}
void 后序遍历(_Node *node){
if(node == nullptr) return;
后序遍历(node->lChild);
后序遍历(node->rChild);
printf("num = %d\n",node->num);
}
|
例如下面的二叉树
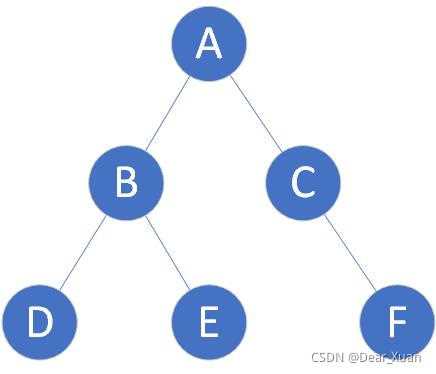
它的遍历顺序分别为
- 前序遍历: A-B-D-E-C-F
- 中序遍历: D-B-E-A-C-F
- 后序遍历: D-E-B-F-C-A
广度优先遍历 BFS
广度优先遍历是指先遍历顶点V的所有子节点V1,V2……Vn,然后再分别遍历V1,V2……Vn的子节点.即每次先遍历完第n层的节点,再遍历n+1层的节点
上图的广度优先遍历顺序为: A-B-C-D-E-F
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| #include <iostream>
#include <queue>
using namespace std;
struct _Node{
int num;
_Node *lChild;
_Node *rChild;
};
void BFS(_Node *node);
int main(){
_Node *nodes[6];
for(int i=0;i<6;i++){
nodes[i] = (_Node*)malloc(sizeof(_Node));
nodes[i]->num = i;
nodes[i]->lChild = nodes[i]->rChild = NULL;
}
nodes[0]->lChild = nodes[1];
nodes[0]->rChild = nodes[2];
nodes[1]->lChild = nodes[3];
nodes[1]->rChild = nodes[4];
nodes[2]->rChild = nodes[5];
BFS(nodes[0]);
return 0;
}
void BFS(_Node *node){
if(node == NULL) return;
_Node *head;
queue<_Node*> q;
q.push(node);
while (!q.empty()){
head = q.front();
q.pop();
printf("Search: %d\n",head->num);
if(head->lChild != NULL) q.push(head->lChild);
if(head->rChild != NULL) q.push(head->rChild);
}
}
|

复杂度与效率
在查找路径时,BFS能够快速找到最短路径,但是它的空间复杂度更高,而DFS也可以找到一条路径,但是不保证它就是最短路径.如果一定要查找最短路径,那么它就需要遍历所有节点.
Dijikstra算法
设图G的邻接矩阵M,M(i,j)表示i到j的距离,用一个大整数来表示i和j不连通
用二维数组map来表示矩阵M,称map[0][0]为原点
1
2
3
4
5
6
7
8
| #define G 10000
int map[5][5] = {
{0,G,3,G,1},
{G,0,1,G,3},
{3,1,0,2,G},
{G,G,2,0,3},
{1,3,G,3,0}
};
|
其中map[i][j]表示i到j的路程距离,G表示i和j不相邻.G可以使用一个大整数来表示,也可以使用-1来表示,但是这样就需要额外写一个判断语句
用d[i]数组来表示原点到i点的最短路程,并使用map[0]来初始化.此时原点到各点的最短路程就是它和相邻的点之间的距离
在每次循环中,先搜索d数组中最小的元素,并将其标记,下次搜索就会跳过这个元素.记搜到的最小值为min,下标为index,循环判断d[index]和map[index][k]的大小,如果存在d[index] + map[index][k] < d[k],则说明从原点先到index点再到k点比直接到k点路程更短,则将d[k]更新为d[index] + map[index][k]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| #include <iostream>
#include <queue>
#define G 10000
using namespace std;
int map[5][5] = {
{0,G,3,G,1},
{G,0,1,G,3},
{3,1,0,2,G},
{G,G,2,0,3},
{1,3,G,3,0}
};
int d[5];
bool mark[5] = {false,false,false,false,false};
void Dijikstra();
int main(){
memcpy(d,map[0],sizeof d);
Dijikstra();
for(int i=0;i<5;i++){
cout << d[i] << endl;
}
return 0;
}
void Dijikstra(){
for(int i=0;i<5;i++){
d[i] = map[0][i];
}
for(int i=1;i<=5;i++){
int min = G;
int index = 0;
for(int j=0;j<5;j++){
if(!mark[j] && min > d[j]){
min = d[j];
index = j;
}
}
mark[index] = true;
for(int j=1;j<5;j++){
if(map[index][j] != G){
if(d[index] + map[index][j] < d[j]){
d[j] = d[index] + map[index][j];
}
}
}
}
}
|
启发式算法
曼哈顿距离
两点的曼哈顿距离是两点x轴之差的绝对值和y轴之差的绝对值的和,例如(x1,y1)和(x2,y2)之间的曼哈顿距离是(∣x1−x2∣+∣y1−y2∣)
欧式距离
欧式距离就是传统平面直角坐标系中的两点间距离
加权图
在之前的图中,都默认边的长度为1.但是在地图中,两个城市之间的距离是不固定的,也就是说每一条公路都有不同的长度,这就是权.实际上在Dijikstra算法中的图也是加权图
在加权图中每条边都有一个权值,因此通路Γ的长度不再是边的个数,而是通路中所有边的权之和
估值函数
设当前访问的顶点为N,终点为G,为了估计N与G的距离,定义估值函数h(N)表示N到G的估计最小距离,而h∗(N)表示N到G的实际最小距离.在平面直角坐标系中,通常用欧式距离来计算h(N),即h(N)=∣NG∣.但是有时为了方便,也可以使用曼哈顿距离来表示h(N)
以地图上的城市为例,在不知道实际最小距离的情况下,通常用连接两城市的线段长度来估计距离,而它们的实际最小距离通常会大于估计最小距离
综合优先级
设图的起点为S,当前访问节点为N,终点为G,显然S到G的实际距离是已知的(只需要把路径上的所有边的权相加).记g(N)为S到N的最小距离,这个最小距离就是所有边的权之和.
记f(N)=g(N)+h(N)为N点的综合优先级,f(N)越小则综合优先级越高
优先队列
优先队列用于保存元素的优先级
例如
数字越小表示优先级越高
A*算法
A∗算法的效率取决于f(N)的准确度,也就是h(N)的准确度
首先将起点放入队列中,记录它的父节点(NULL),g(S)和f(S),然后开始循环:如果队列不为空,则查找优先级最高的点N,遍历与它相邻的所有点,且每个点只被遍历一次,记录下这些点的父节点(N),g(S)和f(S),然后添加到优先队列中,并从优先队列移除N.如此重复,直到终点变成优先级最高的节点,此时从终点G开始,沿着父节点查找就可以找到S到G的最短路径
A*算法示例
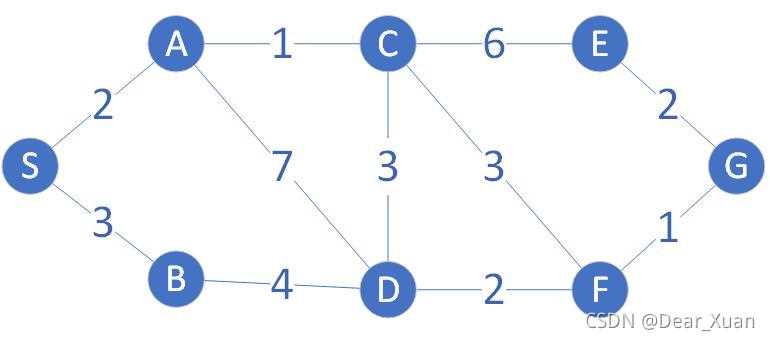
如上图,起点为S,终点为G.为了方便计算,令h(N)=1
先把S加入队列
将与S相邻的节点加入队列,并移除S
A的优先级最高,因此遍历与A相邻的节点,并加入优先队列
| 父节点 | NULL | S | S | A | A | | | | |
| 节点 | S | A | B | C | D | | | | |
| 优先级 | 1 | 3 | 4 | 4 | 10 | | | | |
现在B和C的优先级相同,任意选择一个即可.现选择B作为下一个循环的节点,发现B附近的节点D已经在优先队列中,但是优先级比从A到D更高,因此直接更新列表,覆盖原来的节点
| 父节点 | NULL | S | S | A | B | | | | |
| 节点 | S | A | B | C | D | | | | |
| 优先级 | 1 | 3 | 4 | 4 | 8 | | | | |
选择C作为下一个循环的节点,再次更新D节点
| 父节点 | NULL | S | S | A | C | C | C | | |
| 节点 | S | A | B | C | D | E | F | | |
| 优先级 | 1 | 3 | 4 | 4 | 7 | 10 | 7 | | |
选择D作为下一个循环的节点,由于A,C节点都被遍历过,只需要考虑F,但是从D到F的优先级为9,而从C到F的优先级为7,因此不更新列表
| 父节点 | NULL | S | S | A | C | C | C | | |
| 节点 | S | A | B | C | D | E | F | | |
| 优先级 | 1 | 3 | 4 | 4 | 7 | 10 | 7 | | |
选择F作为下一个节点
| 父节点 | NULL | S | S | A | C | C | C | F | |
| 节点 | S | A | B | C | D | E | F | G | |
| 优先级 | 1 | 3 | 4 | 4 | 7 | 10 | 7 | 8 | |
此时G变成优先级最高的节点,循环结束,沿着父节点一路向上查找,得到的就是最短路径
S-A-C-F-G,g(G)=7,即路径长度为7
估值函数对A*算法的影响
当h(N)=0时,优先级完全由g(N)决定,此时A∗算法变成Dijkstra算法
当h(N)偏小时,意味着某些优先级较低的节点优先级变高,这样会导致循环次数增加,查找范围增大,但是仍然能够找到最短路径
当h(N)偏大时,某些优先级较高的节点优先级降低,可能会导致算法提前终止,查找范围变小,则此时A∗不一定能找到最短路径











