人工智能基础-图论初步

图的基本概念

有序对和无序对

设A,B为任意两个集合,则称$\{\{a,b\}|a∈AΛb∈B\}$为A和B的无序积,记作$A\&B$,$\{a,b\}$为无序对,且对于任意a,b,均有$\{a,b\} = \{b,a\}$

同样的条件下,记$<a,b>$为有序对,它也可以写成集合的形式$\{\{a\},\{a,b\}\}.<a1,b1>=<a2,b2>$当且仅当$a_1=a_2Λb_1=b_2$

无向图

定义无向图G为一个有序的二元组$<V,E>$

V是非空有穷集,称为顶点集,里面的元素称为顶点

E是可以为空的有穷集,称为边集,里面的元素称为无向边(简称 边)

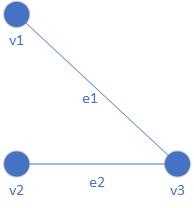
上图中,

$e_1=\{v_1,v_3\},e_2=\{v_2,v_3\}$

$V=\{v_1,v_2,v_3\},E=\{e_1,e_2\}$

$<V,E>$即为无向图$G$

有向图

为无向图的每一条边加上方向,使其由无序对变成有序对,则原无向图变成有向图

需要注意的是,有向图中的E是笛卡尔积V×V的有穷多重子集.E中的元素称为有向边

图的属性

通常用G表示无向图,用D表示有向图.但也可以用G来泛指图

$V(G)$和$E(G)$分别表示G的顶点集和边集,$|V(G)|$和$|E(G)|$分别表示$G$的顶点数和边数

对于有n个顶点的图G,我们称顶点数为G的阶,G为n阶图

对于E为空集的图,我们称它为零图.如果该图只有一个顶点,则称它为1阶零图,也称为平凡图

环

在无向图G中,如果存在$e=\{v_1,v_2\}$,则称$v_1$和$v_2$相邻,且$v_1$,$v_2$是e的端点.如果$v_1=v_2$,则称e为环.

如果存在$e_1=\{v_1,v_2\},e_2=\{v_2,v_3\}$,则称$e_1$和$e_2$相邻

度

顶点$v$作为边的端点的次数称为$v$的度,记作$d(v)$

在有向图中,v作为边的起点的次数之和为v的出度,作为边的终点的次数之和为v的入度,分别记为$d^-(v)$和$d^+(v)$.$d(v)=d^-(v) + d^+(v)$

如果$d(v)$为奇数,称$v$为奇度点,反之为偶度点.如果$d(v)=1$,则称$v$为悬挂顶点

通路与回路

G中顶点与边的交替序列Γ称为通路

如上面的图片中,$Γ=[v_1,e_1,v_3,e_2,v_2]$为$v_1$到$v_2$的通路.$v_1$为始点,$v_2$为终点.当始点就是终点时,称通路$Γ$为回路.它在图中的直观体验就是走了一圈又走回来了.如果$Γ$中出现重复的边,则$Γ$又被称为复杂通路或复杂回路

在无向图中,如果顶点$u,v$之间存在通路,则称$u,v$是连通的.如果图G中的任意两点都是连通的,则称G为连通图,否则为非联通图

在有向图中,如果存在从顶点u到v的边,则称u可达v,记作$u→v$,其中v总是可达自己

如果$u→v$且$v→u$,则称u和v是相互可达的,记作$u↔v$

记$d<u,v>$是从u到v的最短通路

如果一个有向图D的基图是连通图,那么称D为弱连通图,如果对于任意$u,v∈V$,$u→v$和$v→u$至少成立一个,则D为单向连通图,如果两者总是成立,则D为强连通图

树

无向树

设$G=<V,E>$是n阶m条边的无向图,那么下面的命题都是等价的,也就是说只要知道其中一个就能推出别的所有命题

1. G是树
2. G中任意两个顶点存在唯一路径
3. G中无回路且$m=n-1$
4. G中是连通的且$m=n-1$
5. G中没有回路,但是在任意两个不同的顶点之间加一条边后所得的图中有唯一的一个含新边的圈

森林

如果一个无向图G的所有连通分支都是树,则称G为森林.一棵树也是森林

有向树

如果一个有向图的基图是无向树,则称这个有向图为有向树

根树

如果有向树中有且只有一个顶点的入度为0,其它顶点的入度都是1,则称这个有向树为根树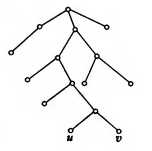

在根树中,如果存在边$e=<u,v>$,则称u为v的父亲,v为u的儿子,如果u可达v$(u≠v)$,则称u为v的祖先,v为u的后代

每个顶点都是一个分支点,如果每个分支点至多有n个儿子,则称这个根树为n叉树

二叉树

二叉树的概念

二叉树是根树中的一个重要结构,它的每个顶点都至多有2个子树,且有左右之分,称为左子树和右子树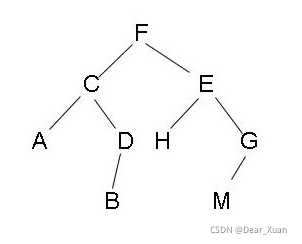

二叉树的遍历

按照一定的规则和顺序走遍二叉树的所有结点,且每个结点只被访问一次,称为遍历